Geometride eksantriklik bir konik kısmın özelliklerini belirtmek için kullanılan bir terimdir, genel olarak e harfi ile gösterilir. Eksantrikliğin, kabaca sözü edilen konik kısmın çemberden ne kadar farklı olduğunu gösteren bir sayı olduğu söylenebilir. Konik kısımlarda:
- Çemberin eksantrikliği 0,
- Elipslerin eksantrikliği 0 ve 1 arasında,
- Parabolün eksantrikliği 1,
- Hiperbolün eksantrikliği 1'den büyük,
- 3 boyutlu sekillerin eksantrikliği 2 boyutlu eksantrik çifti olarak söylenir [2,3] gibi,
- Düz bir çizginin eksantrikliği ise sonsuzdur.

Gök mekaniğinde yörünge veya yörünge hareketi, bir gezegenin yıldız etrafındaki veya bir doğal uydunun gezegen etrafındaki veya bir gezegen, doğal uydu, asteroit veya lagrange noktası gibi uzaydaki bir nesne veya konum etrafındaki yapay uydunun izlediği kavisli bir yoldur. Yörünge, düzenli olarak tekrar eden bir yolu tanımlamakla birlikte, tekrar etmeyen bir yolu da ifade edebilir. Gezegenler ve uydular Kepler'in gezegensel hareket yasalarında tanımlandığı gibi, kütle merkezi elips biçiminde izledikleri yolun odak noktasında olacak şekilde yaklaşık olarak eliptik yörüngeleri takip ederler.

Astrodinamikte, bir astronomik cismin yörünge eksantrikliği, başka cisim etrafındaki yörüngesinin mükemmel bir daireden ne kadar saptığını belirleyen boyutsuz bir parametredir.

Geometride büyük eksen, bir elipsin en uzun çapıdır. Merkezden ve her iki odak noktasından geçen ve çevre uzunluğunun (perimetre) en uzak noktalarında sonlanan bir doğru parçasıdır. Yarı büyük eksen, en uzun yarıçap veya büyük eksenin yarısıdır ve bu nedenle merkezden bir odağa ve çevreye doğru uzanır. Bir elips veya hiperbolün yarı küçük ekseni, yarı büyük eksenle dik açı yapan ve bir ucu konik kesitin merkezinde olan bir doğru parçasıdır. Bir dairenin özel durumu için yarı eksen uzunluklarının her ikisi de dairenin yarıçapına eşittir.

Pergeli Apollonius, konik kesitler üzerindeki çalışmaları ile tanınan Antik Yunan geometri uzmanı ve astronom. Öklid ve Arşimet'in konuya katkılarından başlayarak, onları analitik geometrinin icadından önceki duruma getirdi. Elips, parabol ve hiperbol terimlerinin tanımları bugün kullanımda olanlardır.

Geometride, elips bir koninin bir düzlem tarafından kesilmesi ile elde edilen düzlemsel, ikinci dereceden, kapalı eğridir.

Konik kesit, eliptik veya dairesel bir çift taraflı koninin, düzlemle kesitinden meydana gelen eğriler. Bunlar, çember, elips, parabol ve hiperboldür.

Koni, matematikte, bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekil.

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax2+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.
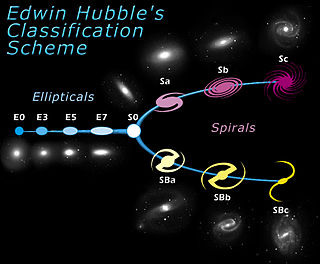
Biçimsel galaksi sınıflandırması, astronomların gökadaları görünüşlerine göre gruplara ayırdıkları bir sınıflandırma sistemidir. Gökadaları görünüşlerine göre sınıflandırmak için kullanılan birkaç şema bulunmaktadır. Bunların en bilineni Edwin Hubble tarafından tasarlanan ve Gérard de Vaucouleurs ile Allan Sandage tarafından genişletilen Hubble düzenidir. Gökada sınıflandırması ve morfolojisi artık büyük ölçüde hesaplama yöntemleri ve fiziksel morfoloji kullanılarak yapılır.

Apsis, gök mekaniğinde, eliptik yörüngedeki bir cismin genelde sistemin kütle merkezi durumunda da olan çekim merkezine yörünge boyunca en yakın ve en uzak olduğu noktalara verilen addır.

Kepler'in gezegensel hareket yasaları, Güneş Sisteminde bulunan gezegenlerin hareketlerini açıklayan üç matematiksel yasadır. Alman matematikçi ve astronom Johannes Kepler (1572-1630) tarafından keşfedilmişlerdir.

Pi5 Orionis (π5 Ori, π5 Orionis), Avcı takımyıldızı yönünde yaklaşık olarak 1.301 ışık yılı uzaklıkta bulunan ikili yıldız sistemidir. Büyüklüğü 3,72 kadirdir ve tek bir nesne gibi görünür, ayrıca 5 Orionis ile görsel bir çift oluştururlar.
Aşağıdaki iyi-tanımlanmış bazı matematiksel şekillerin listesidir.
Hiperbol bir konik kesiti türü. Diğer üç konik kesit türü gibi - parabol, elips ve çember - bir koni ve bir düzlemin kesişimi ile oluşan bir eğridir.

Yörünge mekaniği veya astrodinamik, roketler ve diğer uzay araçlarının hareketini ilgilendiren pratik problemlere, balistik ve gök mekaniğinin uygulamasıdır. Bu nesnelerin hareketi genellikle Newton'un hareket kanunları ve Newton'un evrensel çekim yasası ile hesaplanır. Bu, uzay görevi tasarımı ve denetimi altında olan bir çekirdek disiplindir. Gök mekaniği; daha genel olarak yıldız sistemleri, gezegenler, uydular ve kuyruklu yıldızlar gibi kütle çekimi etkisinde bulunan yörünge sistemleri için geçerlidir. Yörünge mekaniği; uzay araçlarının yörüngelerine ait yörünge manevraları, yörünge düzlemi değişiklikleri ve gezegenler arası transferler gibi kavramlara odaklanır ve itici manevralar sonuçlarını tahmin etmek için görev planlamacıları tarafından kullanılır. Genel görelilik teorisi, yörüngeleri hesaplamak için Newton yasalarından daha kesin bir teoridir ve doğru hesaplar yapmak ya da yüksek yerçekimini ihtiva eden durumlar söz konusu olduğunda bazen gereklidir.
Matematiksel nesneler, matematikte karşılaşılan soyut kavramlara denir. Matematiğin alışıldık dilinde nesne, formal olarak tanımlanmış veya tanımlanabilecek ve matematiksel kanıtlarda kullanılabilecek herhangi bir şey olabilir. Her matematik dalının kendi nesneleri vardır, bu dallara göre bazı örnekler:

Geometride, çevre açı, çember üzerinde iki sekant (kesen) çizgisi kesiştiğinde bir çember üzerinde oluşan açıdır. Çember üzerindeki bir nokta ile çember üzerinde verilen diğer iki noktanın oluşturduğu açı olarak da tanımlanabilir.


















