Komut kümesi mimarisi, CPU'nun yazılım tarafından nasıl kontrol edileceğini tanımlayan bilgisayar soyut modelinin bir parçasıdır. ISA, işlemcinin ne yapabileceğini ve bunu nasıl yapacağını belirterek donanım ve yazılım arasında bir arayüz gibi davranır.
Bilişim, bilişim bilimi ya da bilgisayar bilimi, bilgi ve hesaplamanın kuramsal temellerini ve bunların bilgisayar sistemlerinde uygulanabilmeleri sağlayan pratik teknikleri araştıran bir yapısal bilim dalıdır. Bilişimciler ya da bilgisayar bilimcileri bilgi oluşturan, tanımlayan ve dönüştüren algoritmik süreçler icat edip, kompleks sistemleri tasarlamak ve modellemek için uygun soyutlamalar formüle ederler. Bilişim Dünya'da hızla gelişmeye devam eden önemli bir teknolojidir.
AES, elektronik verinin şifrelenmesi için sunulan bir standarttır. Amerikan hükûmeti tarafından kabul edilen AES, uluslararası alanda da defacto şifreleme (kripto) standardı olarak kullanılmaktadır. DES'in yerini almıştır. AES ile tanımlanan şifreleme algoritması, hem şifreleme hem de şifreli metni çözmede kullanılan anahtarların birbiriyle ilişkili olduğu, simetrik-anahtarlı bir algoritmadır. AES için şifreleme ve şifre çözme anahtarları aynıdır.
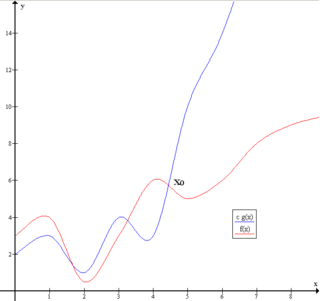
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.
Paralel hesaplama ya da Koşut hesaplama, aynı görevin, sonuçları daha hızlı elde etmek için çoklu işlemcilerde eş zamanlı olarak işletilmesidir. Bu fikir, problemlerin çözümünün ufak görev parçalarına bölünmesi ve bunların eş zamanlı olarak koordine edilmesine dayanır. Paralel hesaplama ile performans artar, büyük sorunlar daha az sürede çözülür ve bilimdeki gelişmeler paralel hesaplamaya gereksinim duyar.
Veri yapısı, bilgisayar ortamında verilerin etkin olarak saklanması ve işlenmesi için kullanılan yapı.
Kolmogorov karmaşıklığı, bilgisayar biliminde, bir metin parçası gibi bir nesneyi tanımlamak için kullanılması gereken bilgi işlemsel kaynakların ölçüsü.
Başlangıçta sonsuz küçük hesap veya "sonsuz küçüklerin hesabı" olarak adlandırılan kalkülüs, geometrinin şekillerle çalışması ve cebirin aritmetik işlemlerin genellemelerinin incelenmesi gibi, kalkülüs sürekli değişimin matematiksel çalışmasıdır.
Ayrık Fourier Dönüşümü, Fourier analizinde kullanılan özel bir Fourier dönüşümüdür.
Birleşmeli Sıralama, bilgisayar bilimlerinde 
derecesinde karmaşıklığa sahip bir sıralama algoritmasıdır. Girdi olarak aldığı diziyi en küçük hale gelene kadar ikili gruplara böler ve karşılaştırma yöntemi kullanarak diziyi sıralar.
Sıralama algoritması, bilgisayar bilimlerinde ya da matematikte kullanılan, verilen bir listenin elemanlarını belirli bir sıraya sokan algoritmadır. En çok kullanılan sıralama türleri, sayı büyüklüğüne göre sıralama ve alfabetik sıralamadır. Sıralama işleminin verimli yapılması, arama ve birleştirme algoritmaları gibi çalışması için sıralanmış dizilere gereksinim duyan algoritmaların başarımının yüksek olması için önemlidir. Sıralama algoritmaları bilgisayarlarda tutulan verilerin düzenlenmesini ve insan kullanıcı tarafından daha rahat algılanmasını da sağlar.
Gustafson yasası, yeterince büyük bir sorunun verimli bir biçimde koşutlaştırılabileceğini öngören bir bilgisayar mühendisliği yasasıdır. 1988 yılında John L. Gustafson'un geliştirdiği bu kural, bir programın koşutluk derecesine bağlı olarak ne ölçüde hızlandırılabileceğini belirleyen Amdahl yasası ile yakından ilintilidir.
Makine öğrenimi (ML), veriden öğrenebilen ve görünmeyen verilere genelleştirebilen ve dolayısıyla açık talimatlar olmadan görevleri yerine getirebilen istatistiksel algoritmaların geliştirilmesi ve incelenmesiyle ilgilenen, yapay zekâda akademik bir disiplindir. Makine öğrenimi, bilgisayarların deneyimlerinden öğrenerek karmaşık görevleri otomatikleştirmeyi sağlayan bir yapay zeka alanıdır. Bu, veri analizi yaparak örüntüler tespit etme ve tahminlerde bulunma yeteneğine dayanır. Son zamanlarda yapay sinir ağları, performans açısından önceki birçok yaklaşımı geride bırakmayı başardı.
Hesaplamalı fizik, fizik sorunlarını çözebilmek için sayısal algoritmaların üretilmesi ve gerçeklenmesini içerir. Genelde kuramsal fizikin bir alt dalı olarak değerlendirilir ancak bazen de kuramsal ve deneysel fizik arasında orta bir dal olarak da düşünülür.
Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.
Hesaplamalı kimya, kimya problemlerini çözmeye yardımcı olmak için bilgisayar simülasyonunu kullanan bir kimya dalıdır. Moleküllerin, katıların yapı ve özelliklerini hesaplamak için verimli bilgisayar programlarına dahil edilmiş teorik kimya yöntemlerini kullanır. Bu yöntemlerin kullanılmasının nedeni, hidrojen moleküler iyonu ile ilgili nispeten yeni sonuçlar dışında, kuantum çok-gövdeli(many-body) problemlerin analitik olarak çözülemez oluşudur. Hesaplama sonuçları normal olarak kimyasal deneylerle elde edilen bilgileri tamamlarken, bazı durumlarda gözlemlenmeyen kimyasal olayları da tahmin edebilmektedir. Yeni ilaç ve materyallerin tasarımında yaygın olarak kullanılmaktadır.
Hesaplamalı geometri, geometri açısından ifade edilebilen algoritmaların incelenmesine ayrılmış bilgisayar bilimlerinin bir dalıdır. Bazı çalışmalar tamamen geometrik problemlerden meydana gelirken bazıları ise hesaplamalı geometrik algoritmaların incelenmesi sonucunda meydana gelmektedir. Bunun gibi problemlerin hesaplama geometrisinin bir parçası olduğu düşünülmektedir. Modern hesaplamalı geometri son zamanlarda gelişme göstermesine karşın, tarihin antik dönemine kadar uzanan en eski bilgi işlem alanlarından biridir.
Bilimsel hesaplama karmaşık problemleri anlamak ve çözmek için gelişmiş bilgi işlem yeteneklerini kullanan çok disiplinli bir alandır. Hesaplamalı bilim üç farklı unsuru birleştirmektedir:
Kriptografide, scrypt, Colin Percival tarafından Tarsnap çevrimiçi yedekleme hizmeti için oluşturulan bir parola tabanlı anahtar türetme fonksiyonudur. Bu algoritma, büyük miktarda bellek gerektirerek büyük ölçekli özel donanım saldırılarını gerçekleştirmeyi pahalı hale getirmek için özel olarak tasarlanmıştır. 2016 yılında, scrypt algoritması IETF tarafından RFC 7914 olarak yayınlandı. Scrypt algoritmasının, ArtForz kullanıcı adına sahip ve gerçek adı bilinmeyen bir programcı tarafından implemente edilmiş, basitleştirilmiş bir sürümü, önce Tenebrix'te ve ardından Fairbrix ve Litecoin olmak üzere bir dizi kripto para birimi tarafından iş kanıtı şeması olarak kullanıldı.
Teorik bilgisayar biliminde, zaman karmaşıklığı bir algoritma çalıştırmak için gereken bilgisayar zamanını tanımlayan hesaplama karmaşıklığıdır. Zaman karmaşıklığı genellikle algoritma tarafından gerçekleştirilen temel işlemlerin sayısı sayılarak ve her bir temel işlemin gerçekleştirilmesinin sabit bir zaman aldığı varsayılarak tahmin edilir. Böylece, algoritma tarafından gerçekleştirilen temel işlemlerin sayısı ile harcanan zamanın bir sabit faktör ile ilişkili olduğu kabul edilir.
