İçeriğe atla

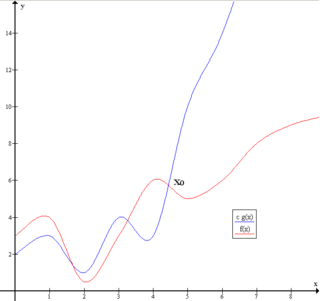
Algoritma

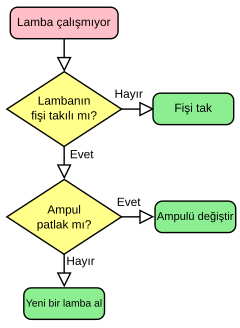
Algoritmaları daha kolay anlatabilmek için akış şemaları kullanılır.

Algoritma, belli bir problemi çözmek veya belirli bir amaca ulaşmak için tasarlanan yol.[1][2] Matematikte ve bilgisayar biliminde bir işi yapmak için tanımlanan, bir başlangıç durumundan başladığında, açıkça belirlenmiş bir son durumunda sonlanan, sonlu işlemler kümesidir. Genellikle bilgisayar programlamada kullanılır ve tüm programlama dillerinin temeli algoritmaya dayanır. Aynı zamanda algoritma tek bir problemi çözecek davranışın, temel işleri yapan komutların veya deyimlerin adım adım ortaya konulmasıdır ve bu adımların sıralamasına dikkat edilmelidir. Bir problem çözülürken algoritmik ve sezgisel (herustic) olmak üzere iki yaklaşım vardır. Algoritmik yaklaşımda da çözüm için olası yöntemlerden en uygun olan seçilir ve yapılması gerekenler adım adım ortaya konulur. Algoritmayı belirtmek için; metinsel olarak düz ifade ve akış diyagramı olmak üzere 2 yöntem kullanılır. Algoritmalar bir programlama dili vasıtasıyla bilgisayarlar tarafından işletilebilirler.

İlk algoritma, el-Hârizmî tarafından "Hisab el-cebir ve el-mukabala" kitabında sunulmuştur. Algoritma sözcüğü de el-Hârizmî'nin isminin Avrupalılarca telaffuzundan doğmuştur.[3]

Tarihi

Algoritma sözcüğü Ebu Abdullah Muhammed bin Musa el Harezmi'nin Latince isminden kaynaklanır.
Ana madde: Algoritmaların tarihsel sıralaması

Algoritma sözcüğü, Özbekistan'ın Harezm, bugünkü Türkmenistan'ın Hive kentinde doğmuş olan Ebu Abdullah Muhammed İbn Musa el Harezmi'den gelir.[4][5] Bu alim 9. yüzyılda cebir alanındaki algoritmik çalışmalarını kitaba dökerek matematiğe çok büyük bir katkı sağlamıştır. "Hisab el-cebir ve el-mukabala (حساب الجبر و المقابلة)" kitabı dünyanın ilk cebir kitabı ve aynı zamanda ilk algoritma koleksiyonunu oluşturur. Latince çevirisi Avrupa'da çok ilgi görür. Alimin ismini telaffuz edemeyen Avrupalılar "algorizm" sözcüğünü "Arap sayıları kullanarak aritmetik problemler çözme kuralları" manasında kullanırlar. Bu sözcük daha sonra "algoritma"ya dönüşür ve genel kapsamda kullanılır.

Uygulama

Çoğu algoritmalar bilgisayar olarak uygulanmak üzere tasarlanmıştır. Bununla birlikte, başka yöntemlerle de uygulanmaktadır, biyolojik sinir ağı (örneğin insan beyninin hesap yapması veya bir böceğin yemek araması), elektrik devresi veya mekanik cihazlar gibi.

Bilgisayar algoritmasına örnek verelim. Kullanıcının girdiği dört sayının ortalamasını görüntüleyen algoritmayı yazalım: 

 A0 --> Başla
 A1 --> Sayaç=0 (Sayaç'ın ilk sayısı 0 olarak başlar.)
 A2 --> Sayı=? : T=T+Sayı (Sayıyı giriniz. T'ye sayıyı ekle ve T'yi göster.)
 A3 --> Sayaç=Sayaç+1 (Sayaç'a 1 ekle ve sayacı göster.)
 A4 --> Sayaç<4 ise A2'ye git. (Eğer sayaç 4'ten küçükse Adım 2'ye git.)
 A5 --> O=T/4 (Ortalama için T değerini 4'e böl)
 A6 --> O'yu göster. (Ortalamayı göster.)
 A7 --> Dur
Rastgele üretilmiş değerler dizisini quicksort algoritması kullanarak küçükten büyüğe artarak sıralanması.
Quicksort sıralama algoritması animasyonu. Animasyonun başında kırmızı çubukların pivot elemanı olarak işaretlendiği görülmektedir. Örneğin başında sağ tarafın en uzak elemanı pivot olarak seçilmiştir. Bu seçilen pivot değerleri parçalara ayrılmış değerler kümesinin elemanlarıyla karşılaştırılıp sıralama sağlanmaktadır. Özetle, sıralanacak bir sayı dizisini daha küçük parçalara ayırıp oluşan bu küçük parçaların kendi içinde sıralanması ve birleştirilmesi mantığıyla çalışır.

İkinci dereceden ax² + bx + c = 0 biçiminde bir denklemin tüm köklerini bulmak için algoritma yazalım: 

Adım 1: Başla.
Adım 2: a, b, c, D, x1, x2, rp ve ip değişkenlerini tanımla.
Adım 3: Diskriminant değerini hesapla.
D ← b2-4ac
Adım 4: Eğer D≥0
x1 ← (-b+√D) / 2a
x2 ← (-b-√D) / 2a
değerlerini hesapla ve x1,x2 değişkenleri göster.
Eğer D≥0 değilse,
Gerçek kısım(rp) ve sanal kısmını(ip) hesapla.
rp ← b / 2a
ip ← √ (D) / 2a
Adım 5: "rp + j(ip)" ve "rp - j(ip)" değerlerini göster.
Adım 6: Dur.

Kullanıcı tarafından girilen bir sayının faktöriyel değerini bulmak için bir algoritma yazalım: 

Adım 1: Başla.
Adım 2: factorial,i ve n değişkenlerini tanımla.
Adım 3: Değişkenlerin başlangıç değerlerini tanımla.
factorial ← 1
i ← 1
Adım 4: Ekrandan girilen n değerini oku.
Adım 5: (i=n) eşitliği sağlanana kadar tekrarla.
5.1: factorial←factorial*i
5.2: i←i+1
Adım 6: factorial değişkeninin değerini göster.
Adım 7: Dur.

Hukuki Konular

Algoritmalar, tek başlarına, genellikle patent verilebilir değildirler. Amerika Birleşik Devletleri'nde soyut kavramların, sayıların ve işaretlerin yalnızca basit yönlendirmelerinden oluşan bir iddia "süreç" oluşturmaz (USPTO 2006) ve bundan dolayı algoritmalar patent verilebilir değildir (Gottschalk v.Benson'da olduğu gibi). Bununla birlikte, algoritmanın pratik uygulamaları zaman zaman patent verilebilirdir. Örneğin, Diamond v.Diehr'da, sentetik kauçuğun muhafaza edilmesine yardımcı olmak için kullanılan basit geri bildirim algoritmasının uygulaması patent verilebilir sayılmıştır. Yazılım patenti son derece tartışmalıdır ve algoritmaları içeren birçok eleştirilmiş patent vardır, özellikle veri sıkıştırma algoritmaları, Unisys' LZW patentinde olduğu gibi.

Ek olarak, bazı kriptografik algoritmaların ihracat kısıtlamaları vardır.

1950'den Sonraki Tarihi

Faaliyetlerin birçoğu algoritmanın tanımının geliştirilmesine yönlendirilmiştir ve aktifliği çevredeki sorunlar nedeniyle, özellikle matematiğin temelleri (özellikle Church-Turing tezi) ve akıl felsefesi (özellikle yapay zeka konusundaki tartışmalar) sebebiyle devam etmiştir.

Algoritmalara eleştirel yaklaşımlar

Algoritmaların kullanımı hayatın her alanında giderek yaygınlaşmaktadır. İş yerlerindeki performans değerlendirmelerinden bankaların kime kredi vereceğine, güvenlik sistemlerinden sosyal medya platformlarındaki önerilere kadar hayatın her alanında etkili olan algoritmalara özellikle de sosyal bilimci akademisyenler çeşitli eleştiriler yöneltmektedir. Algoritmaların teknolojik etkilerinin yanı sıra toplumsal bir güce de sahip oldukları,[6] toplumsal gruplar arasındaki eşitsizlikleri derinleştirdikleri,[7] yeni güç dengeleri oluşturdukları[8] ve farklı otoriteler tarafından toplumun belli kesimlerini baskılamak[9] için kullanıldıklarının altı çizilmektedir.

Önemli algoritma türleri

  • Arama algoritmaları
  • Bellek yönetimi algoritmaları
  • Bilgisayar grafiği algoritmaları
  • Birleşimsel algoritmalar
  • Çizge algoritmaları
  • Evrimsel algoritmalar
  • Genetik algoritmalar
  • Kripto algoritmaları veya kriptografik algoritmalar
  • Kök bulma algoritmaları
  • Optimizasyon algoritmaları
  • Sıralama algoritmaları
  • Veri sıkıştırma algoritmaları

Ayrıca bakınız

Kaynakça

  1. ^ "The Definitive Glossary of Higher Mathematical Jargon — Algorithm". Math Vault (İngilizce). 1 Ağustos 2019. 7 Şubat 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Kasım 2019. 
  2. ^ "Definition of ALGORITHM". Merriam-Webster Online Dictionary (İngilizce). 14 Şubat 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Kasım 2019. 
  3. ^ "Al-Khwarizmi - Islamic Mathematics". The Story of Mathematics. 25 Temmuz 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 14 Kasım 2019. 
  4. ^ "Al-Khwarizmi biography". www-history.mcs.st-andrews.ac.uk. 2 Ağustos 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 27 Şubat 2020. 
  5. ^ "Etymology of algorithm". Chambers Dictionary. 31 Mart 2019 tarihinde kaynağından arşivlendi. Erişim tarihi: 13 Aralık 2016. 
  6. ^ Beer, David (2 Ocak 2017). "The social power of algorithms". Information, Communication & Society. 20 (1): 1-13. doi:10.1080/1369118X.2016.1216147. ISSN 1369-118X. 
  7. ^ author., Eubanks, Virginia, 1972-. Automating inequality : how high-tech tools profile, police, and punish the poor. ISBN 1-250-21578-1. OCLC 1050280177. 
  8. ^ Masso, Anu; Kasapoglu, Tayfun (2 Temmuz 2020). "Understanding power positions in a new digital landscape: perceptions of Syrian refugees and data experts on relocation algorithm". Information, Communication & Society. 23 (8): 1203-1219. doi:10.1080/1369118X.2020.1739731. ISSN 1369-118X. 
  9. ^ author., Noble,. Algorithms of Oppression. ISBN 978-1-4798-6676-2. OCLC 1124443189. 

İlgili Araştırma Makaleleri

Cebir sayılar teorisini, geometriyi ve analizi içine alan geniş bir matematik dalıdır. Temel matematik işlemlerinden, çember ve daire alanları bulmayı kapsayan geniş bir ilgi alanına sahiptir. Cebir, mühendislik ve eczacılık gibi birçok alanda kullanılmaktadır. Kuramsal cebir, ileri matematiğin bir dalı olmakla birlikte sadece uzmanlar tarafından çalışılan bir koldur.

<span class="mw-page-title-main">Hârizmî</span> Fars matematikçi, astronom ve coğrafyacı

Hârizmî ya da tam künyesiyle Ebû Ca'fer Muhammed bin Mûsâ el-Hârizmî ; matematik, gök bilim, coğrafya ve algoritma alanlarında çalışmış Fars bilim insanı. Hârizmî 780 yılında Harezm bölgesinin Hive şehrinde dünyaya gelmiştir. 850 yılında Bağdat'ta ölmüştür.

<span class="mw-page-title-main">İstatistik</span>

İstatistik veya sayım bilimi, belirli bir amaç için veri toplama, tablo ve grafiklerle özetleme, sonuçları yorumlama, sonuçların güven derecelerini açıklama, örneklerden elde edilen sonuçları kitle için genelleme, özellikler arasındaki ilişkiyi araştırma, çeşitli konularda geleceğe ilişkin tahmin yapma, deney düzenleme ve gözlem ilkelerini kapsayan bir bilimdir. Belirli bir amaç için verilerin toplanması, sınıflandırılması, çözümlenmesi ve sonuçlarının yorumlanması esasına dayanır. Bu çerçevede yapılan işlemlerin tümüne sayımlama denir.

<span class="mw-page-title-main">Büyük O gösterimi</span>

Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.

Ortalama veya merkezsel konum ölçüleri, istatistik bilim dalında ve veri analizinde kullanılan bir veri dizisinin orta konumunu, tek bir sayı ile ifade eden betimsel istatistik ölçüsüdür. Günlük hayatta ortalama dendiğinde genellikle kast edilen aritmetik ortalama olmakla beraber bu ölçünün çok belirli bazı dezavantajları söz konusudur. Bu yüzden matematik ve istatistikte, bir anakütle veya örneklem veri dizisi değerlerini temsil eden tek bir orta değer veya beklenen değer, olarak medyan (ortanca), mod (tepedeğer), geometrik ortalama, harmonik ortalama vb adlari verilen birçok değişik merkezsel konum ölçüleri geliştirilmiş ve pratikte kullanılmaktadır.

Merkezi limit teoremi büyük bir sayıda olan bağımsız ve aynı dağılım gösteren rassal değişkenlerin aritmetik ortalamasının, yaklaşık olarak normal dağılım göstereceğini ifade eden bir teoremdir. Matematiksel bir ifadeyle, bir merkezi limit teoremi olasılık kuramı içinde bulunan bir zayıf yakınsama sonucu setidir. Bunların hepsi, birçok bağımsız aynı dağılım gösteren rassal değişkenlerin herhangi bir toplam değerinin limitte belirli bir "çekim gücü gösteren dağılıma" göre dağılım gösterme eğiliminde olduğu gerçeğini önerir.

Matematik biliminde, özellikle yöneylem araştırması uygulamalı dalında, doğrusal programlama problemleri bir doğrusal amaç fonksiyonunun doğrusal eşitlik ve/veya eşitsizlik kısıtlamalarını sağlayacak şekilde optimizasyon yapılmasıdır. Bir optimizasyon modeli eğer sürekli değişkenlere ve tek bir doğrusal amaç fonksiyonuna sahipse ve tüm kısıtlamaları doğrusal eşitlik veya eşitsizliklerden oluşuyorsa, doğrusal (lineer) program olarak adlandırılır. Başka bir deyişle, modelin tek-amaçlı fonksiyonu ve tüm kısıtlamaları, süreklilik gösteren karar değişkenlerinin ağırlıklı toplamlarından oluşmalıdır.

Olasılık teorisi ya da ihtimaliyet teorisi rastgele olayların analizi ile ilgilenen bir matematik bilim dalıdır. Olasılık teorisinin ana ögeleri rassal değişkenler, saf rassal süreçler, olaylar olarak sayılabilir. Bunlar ya tek olarak ortaya çıkan veya bir zaman dönemi içinde gelişerek meydana gelen, ilk görünüşü rastgele bir şekilde olan deterministik olmayan olayların veya ölçülebilir miktarların matematiksel soyutlamalarıdır. Bir madeni parayı yazı-tura denemesi için havaya atmak veya bir zarı atmak ile ortaya çıkan sonuç ilk bakışta rastgele bir olay olarak görülebilirse bile eğer birbirini takip eden rastgele olaylar tekrar tekrar ortaya çıkartılırsa incelenebilecek ve tahmin edilebilecek belirli bir istatistiksel seyir takip ettikleri görülecektir. Bu türlü olaylar ve sonuçların seyirlerini betimleyen iki temsilci matematiksel sonuç büyük sayılar yasası ve merkezsel limit teoremidir.

Olasılık kuramı ve istatistik bilim dallarında, bir rassal değişken X için, eğer beklenen değer var ise, moment üreten fonksiyon şöyle tanımlanır:

Matematik bilimi içinde moment kavramı fizik bilimi için ortaya çıkartılmış olan moment kavramından geliştirilmiştir. Bir bir reel değişkenin reel-değerli fonksiyon olan f(x)in c değeri etrafında ninci momenti şöyle ifade edilir:

<span class="mw-page-title-main">Sayısal analiz</span>

Sayısal analiz, diğer adıyla nümerik analiz veya sayısal çözümleme, matematiksel analiz problemlerinin yaklaşık çözümlerinde kullanılan algoritmaları inceler. Bu nedenle birçok mühendislik dalı ve doğa bilimlerinde önem arz eden sayısal analiz, bilimsel hesaplama bilimi olarak da kabul edilebilir. Bilgisayarın işlem kapasitesinin artması ile gündelik hayatta ortaya çıkan birçok sistemin matematiksel modellenmesi mümkün olmuş ve sayısal analiz algoritmaları burada ön plana çıkmıştır. 21. yüzyıldan itibaren bilimsel hesaplama yöntemleri mühendislik ve doğa bilimleri ile sınırlı kalmamış ve sosyal bilimler ile işletme gibi alanları da etkilemiştir. Sayısal analizin alt başlıklarına adi diferansiyel denklemlerin yaklaşık çözümleri ve özellikle veri biliminde önem taşıyan sayısal lineer cebir ile optimizasyon örnek gösterilebilir.

Döngüsel artıklık denetimi, çoğunlukla sayısal şebekelerde ve depolama cihazlarında kullanılan ve ham veride yapılan hatalı değişimleri algılayan, uygulaması kolay ve güvenliği güçlü bir hata bulma yöntemidir.

<span class="mw-page-title-main">Zaman serisi</span>

Zaman serisi, istatistik, sinyal işleme, ekonometri ve finansal matematikte veri noktalarının sıklığını ifade eder ve düzenli zaman aralıklarında, ardışık zaman alanlarında tipik olarak ölçülür. Zaman serisine örnek olarak, İMKB endeksinin günlük kapanış değeri veya Türkiye'deki Kızılırmak nehrinin yıllık akış hacmi (debisi) verilebilir. Zaman serisi analizi, anlamlı istatistikleri ve verinin diğer istatistiklerini almak için birkaç yöntemi vardır. Zaman serisi tahmini önceden bilinen olayları baz alarak gelecek olayları tahmin etmenin kavramsal modelidir. Ekonometride zaman serisi tahminine bir örnek, önceki başarımlarına (performanslarına) bakarak bir hisse senedinin açılış fiyatını öngörmektir.

SAT problemi bir NP-tam sınıfı problemidir.

Matematiksel model, bir sistemin matematiksel kavramlar ve dil kullanılarak tanımlanmasıdır. Matematiksel model geliştirme süreci, matematiksel modelleme olarak adlandırılır. Matematiksel modeller, doğa bilimlerinde ve mühendislik disiplinlerinde bunun yanı sıra sosyal bilimlerde kullanılır. Matematiksel modelleri daha çok fizikçiler, mühendisler, istatistikçiler, operasyon araştırma analistleri ve ekonomistler kullanır. Model, bir sistemi açıklamaya, farklı bileşenlerin etkilerini incelemeye ve bir davranış hakkında öngörüde bulunmak için yardımcı olabilir.

Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.

<span class="mw-page-title-main">Uluslararası Veri Şifreleme Algoritması</span>

Uluslararası Veri Şifreleme Algoritması (IDEA), 1991 yılında Xuejia Lai ve James Massey tarafından tasarlanmış bir blok şifreleme algoritmasıdır. Bilinen en güçlü algoritmalardandır.

<span class="mw-page-title-main">Parametre</span> belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik

Parametre belirli bir sistemi tanımlamak veya sınıflandırmak için yardımcı olabilecek herhangi bir özellik. Parametre, sistemi tanımlarken veya performansını, durumunu değerlendirirken yararlı veya kritik olan bir sistem unsurudur.

Sembolik matematik; sembolik hesaplama ve cebirsel hesaplamadan oluşan bilgisayar cebrindeki, matematiksel ifadeleri ve diğer matematiksel nesneleri manipüle etmek için kullanılan algoritma ve yazılımların çalışması ve geliştirilmesine atıfta bulunan bilimsel bir alandır.Daha açıkça ifade etmek gerekirse, bilgisayar cebri bilimsel hesaplamanın bir alt alanı sayılır ve bununla beraber bilimsel hesaplama genelde yaklaşık kayan nokta sayılarına ve sayısal yaklaşımlara dayanmaktadır.Buna karşın sembolik hesaplama, hiçbir değişkeni içermeyen ifadelerle tam hesaplamayı vurgulamaktadır.Değişken içermeyen ifadelere ilişkin semboller manipüle edilmektedir ve adı bundan dolayı sembolik matematik olarak kabul edilir.

HMAC Tabanlı Tek Seferlik Parola algoritması (HOTP), özet-tabanlı mesaj doğrulama kodlarına (HMAC) dayanan tek seferlik parola (OTP) algoritmasıdır. Açık Kimlik Doğrulama Girişiminin (OATH) bir temel taşıdır.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.