Akışkanlar mekaniği tarihi
Akışkanlar mekaniğinin tarihi, fizik ve mühendislik tarihinin temel bir koludur. Akışkanların (sıvılar ve gazlar) hareketi ve onlara etki eden kuvvetlerin incelenmesi tarih öncesine kadar uzanmaktadır. İnsanın suya bağımlılığı, meteorolojik koşullar ve iç biyolojik süreçler nedeniyle sürekli bir evrim geçirmiştir.
İlk uygarlıkların başarısı, deniz taşımacılığının yanı sıra su dağıtımı ve çiftlik sulama için kanal ve su kemerlerinin inşasına olanak tanıyan su dinamikleri anlayışındaki gelişmelere atfedilebilir. Kavramsal karmaşıklığı nedeniyle, bu alandaki keşiflerin çoğu, en azından diferansiyel denklemler ve hesaplamalı yöntemlerin ileri düzeyde anlaşılmasının geliştirilmesine kadar neredeyse tamamen deneylere dayanıyordu. Akışkanlar mekaniğini tanımlamak için temel denklemleri geliştiren Arşimet, Johann Bernoulli ve oğlu Daniel Bernoulli, Leonhard Euler, Claude-Louis Navier ve George Gabriel Stokes gibi önemli kişiler tarafından önemli teorik katkılar yapılmıştır. Deneysel ve hesaplamalı yöntemlerdeki gelişmeler, alanı daha da ileriye taşımış ve havacılıktan çevre mühendisliğine kadar daha uzmanlaşmış endüstrilerde pratik uygulamalara yol açmıştır. Akışkanlar mekaniği, astronomik cisimlerin ve galaksilerin dinamiğinin incelenmesi için de önemli olmuştur.
Antik Dönem
Tarih öncesi
Antik medeniyetlerde ok, mızrak, gemi tasarımı ve sulama, taşma gibi genel olarak hidrolik mühendisliği içeren, bilimsel değilse bile pragmatik bilgiler elde edilmişti.[1] En erken insan medeniyetlerinin nehir kıyılarında kurulması su bilimi, hidrolik ve hidrolik mühendisliğinin başlangıcına sebep oldu.
Antik Çin
Özgül ağırlık ve kaldırma kuvveti gözlemleri eski Çin filozofları tarafından kaydedildi. M.Ö. 4. yüzyılda Mensiyüs altının ağırlığının tüylerle eşdeğer olduğunu anlatır. MS 3. yüzyılda Cao Chong, farklı ağırlıklarla yüklü teknelerin yer değiştirmesini gözlemleyerek filin tartılmasının öyküsünü anlatmaktadır.[2]
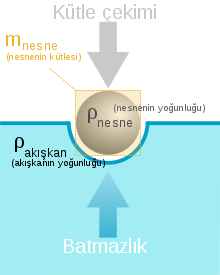
Hidrostatik’in temel prensibi Arşimet tarafından “Yüzen cisimler üzerine” çalışmasında MÖ 250 yılında verilmiştir. Bu çalışmada Arşimet, Arşimet prensibi olarak da bilinen batmazlık yasasını geliştirir. Bu prensip, akışkana batırılan cismin, taşırdığı akışkanın ağırlığına eşit miktarda bir kaldırma kuvvetine maruz kalacağını belirtir.[3] Arşimet, dengede olan bir akışkanın her yönden eşit miktarda bastırıldığını ve bu akışkanda yüzen cismin de denge pozisyonunda olacağını söyler.[4]
İskenderiye'deki Batlamyus'un desteği ile gelişen Yunan okulunda hidrolik makine yapımı için çalışmalar yapıldı. MÖ 120 yılı civarinda Ktesibios ve Heron tarafından tazyikli su çeşmesi, sifon ve piston pompası (forcing-pump) icat edildi.
Sifon oldukça basit bir araçken pompa, hidroliğin bebeklik döneminden beklenilemeyecek kadar karmaşıktır. Pompa, muhtemelen o zamanlar yaygın olan birkaç toprak çömleği bir tekerlek tarafından döndüren güzel bir çeşit zincir pompa (chain pump) olan Mısır tekerleği veya Noria'dan esinlenildi. Bunlardan bazılarında çömleklerin alt kısmında fazla dirence maruz kalmadan alçalarak tekerlek üzerindeki yükü büyük ölçüde azaltan bir vana bulunuyordu. Eğer bu vananın Ktesibios zamanı gibi çok eski bir zamanda tanıtıldığını farz edersek böyle bir makinenin pompa (forcing-pump) gibi karmaşık bir makinenin icadına yol açmasını anlamak çok da zor olmayacaktır.[4]
İskenderiye okulundaki bu icatlara rağmen dikkatlerin akışkanların hareketine yönlenmediği görülüyor. Bu konuyu incelemek için ilk çaba Roma’nın Nerva ve Trajan dönemindeki halk çeşmelerini denetleyen Sextus Julius Frontinus tarafından verilmiştir. De aquaeductibus urbis Romae commentaries adlı çalışmasında o dönemlerde tüplerden boşaltılan suyun miktarını ölçmede kullanılan yöntemler ve su kemerlerindeki ve çeşmelerdeki suyun dağıtılışını inceler. Suyun menfezden akışının sadece deliğin büyüklügüne değil rezervuardaki suyun yüksekliğine de bağlı olduğunu; ve sukemerinden su çekmek için koyulan bir borunun, aşağı-yukarı suyun akışının yönünde koyulması gerektiğini gözlemledi. Ancak menfezin derinliğine bağlı olarak suyun ivmesi yasalarıyla tanışmadığı için sonuçlarındaki kesinlik isteği şaşırtıcı değildir.[4]
Ortaçağ
İslam fizikçileri
İslam coğrafyası bilim adamları, özellikle Abu Rayhan Biruni (973-1048) ve sonradan Al-Khazini (1115-1130) bilimsel metotları akışkan mekaniğine deneylerle uygulayan ilk bilim adamlarındandır. özellikle spesifik ağırlığı belirlemede kullanılan akışkan statiği. Matematikteki oranlar teorisini ve son derece az teknikleri uyguladı. Cebir ve ince hesaplama tekniklerini akışkan statiği alanına tanıtmıştır.[5][Not 1] Akışkan statiğinde Biruni objenin spesifik yerçekimi ve suyun hacmi arasında bir orantı olduğunu keşfetti. Ayrıca deneyler sırasında testleri kontrol etme metodunu tanıttı ve değişik sıvıların özağırlıklarını ölçtü. Tatlı ve tuzlu su, sıcak ve soğuk su arasındaki ağırlık farkını da kaydetti. Akışkan mekaniği üzerine deneyleri suresince cismin havadaki ağırlığı ile yerini aldığı suyun ağırlığı arasındaki oranı bulmak için Biruni konik ölçüyü (conical measure) icat etti.[6]“The Book of the Balance of Wisdom (1121)” kitabında Al-Khazini hidrostatik dengeyi icat ettiğini yazmıştır.[7]
İslam mühendisleri
9. yüzyılda Banu Musa Kardeşler’in ‘Book of Ingenious Devices' kitabı ilk dönemlerde akışkan mekaniğin otomatik kontrolünü tanımlamıştır.[8] İlk kontrollerden biri olan 2-adımlı akışkan kontrolü Banu Musa kardeşler tarafından geliştirilmiştir.[9] Ayrıca akışkanlar için geri beslemeli kontrolü de tanımlamışlardır.[10] Donald Routledge Hill'e’e göre, Banu Musa kardeşler hidrostatik basınç ve akışkan sistemlerdeki “in-line” konik vana kullanımındaki “küçük varyasyonlardan istifade etme" ustalarıdır.[11] Plug vana,[10][11] Şamandıralı vana,[10] musluk gibi diğer vanaların kullanımı da tanımlamışlardır.[12] Banu Musa Kardeşler ayrıca “küçük miktarlarda sıvıyı tekrar tekrar alabilmeyi sağlayan fakat yüksek miktarda alınırsa daha ileri ekstraksiyonun mümkün olmadığı” .emniyet mekanizması geliştirmişlerdir.[11] Antik Yunan çalışmalarında görülmeyen çift-konsentrik sifon ve değişik sıvıların dökülmesinde kullanılan eğik uçlu huni de Banu Musa’nın orijinal icatlarındandır.[12] Yine çalışmalarında diğer mekanizmalardan yüzen depo[8] ve diferansiyel basıncı da tanımlamaktadırlar.[13]
1206'da el-Cezerî’nin “Book of knowledge of ingenious mechanical devices” kitabı birçok hidrolik makineyi tanımlamıştır.[14] Su yükseltme pompası ayrıca önem taşımaktadır. Zincir pompada ilk kez kullanılan krank mili el-Cezerî’nin saqiyah makinesinde de kullanılmıştır. Periyodik çalışmayı en aza indirgeme konsepti de saqiyahzincir pompasının verimini maksimize etmek amacıyla ilk olarak bu makinede uygulanmıştır. El-Cezerî ayrıca ilk emme borularını içeren ikiz-silindirli vargel (reciprocating) pistonu emme pompası, emme pompalama, çift-etki pompalamayı icat etmiş ve vanalar ile krank mili biyel mekanizmalarını ilk defa kullanmıştır.[8][11] Bu pompa üç nedenden dolayı oldukça etkileyicidir;
- Gerçek bir emme borusunun (akışkanı kısmi bir vakuma emen) bir pompada bilinen ilk kullanımı,
- Çift işlev prensibinin ilk uygulaması
- Krank mili biyel kolu mekanizmasını kullanarak devir hareketinin aşağı yukarı harekete çevrimi.
On altıncı ve on yedinci yüzyıllar
Castelli ve Torricelli
Galileo'nun öğrencileri Benedetto Castelli ve Evangelista Torricelli, Galileo'nun prensiplerini hidrodinamiğe uygulamışlardır. Castelli 1628'te akışkanların nehirlerde ve kanallardaki hareketini başarıyla açıklarken, Torricelli, Magiotti'nin deneylerinde ispat ettiği üzere, bir jet içerisinde bir deliğe rastlayan suyun geldiği rezervuardaki yüksekliğe çıktığını gözlemleyip bunun enerjetiğini açıklamıştır.[4]
Blaise Pascal
Pascal’ın ellerinde hidrostatik bir bilim olarak değer kazanırken, ölümünden sonra el yazmaları arasında bulunan ve 1663'te yayınlanan sıvıların dengesi üzerine olan bir incelemede, sıvıların dengesi yasaları en basit şekilde gösterildi ve deneylerle fazlasıyla doğrulanmıştır.[4]
Mariotte ve Guglielmini
Ölümünden sonra yaptığı deneylerin sonucu yayınlanan Edme Mariotte (1620-1684), Torricelli'nin kuramının gözlenmesi ile uğraşmıştır. Gözlemleri yüzeysel olsa dahi, deney ve kuram arasındaki çelişkiyi suyun hızının sürtünmeden kaynaklı yavaşlamasına bağlamasını keşfetmiştir. Bologna’daki nehir ve kanalların denetçisi Domenico Guglielmini (1655-1710), nehirlerdeki hız kaybını nehrin dibindeki eşitsizliklerden kaynaklanan enine hareketlerle ilişkilendirmiştir. Fakat Mariotte aynı yavaşlamayı cam borularda dahi gözlemlediğinden, Guglielmini'nin kuramı temelsiz görülmüştür. Buna paralel, İtalya doğumlu Fransız filozof, bu yavaşlamayı sürtünmeye bağlamıştır. Suyun filamentlerinin boruya sürtünürken hızından kaybettiğini, bunlara bitişik filamentlerinse daha yüksek hıza sahip olduklarından köşedeki filamentleri sürtündüğünü ve bu yüzden yavaşladığını savlamıştır.[4]
On sekizinci yüzyıl
Isaac Newton tarafından yapılan çalışmalar
Sürtünme ve viskozite
Akan suyun hızındaki yavaşlamaya sürtünme ve viskozitenin etkisi Newton’ın Principia’sında yer almaktadır. Kartezyen girdap sisteminin evrensel olarak geçerli olduğu bir zamanda, bu hipotezi araştırmayı gerekli buldu ve araştırmaları sırasında girdabın herhangi bir katmanının hızının, bu katmanların hızları arasında aritmetik bir ortalama olduğunu göstermiştir. Bundan açıkça şu sonuç çıkıyor ki, bir boru içinde hareket eden bir su filamanının hızı, onu çevreleyen filamanların hızları arasındaki aritmetik bir ortalamadır. Bu sonuçlardan yararlanan İtalya doğumlu Fransız mühendis Henri Pitot sürtünme kaynaklı yavaşlamanın sıvının aktığı boruların çapıyla ters orantılı olduğunu göstermiştir.[4]
Delik
Newton’un dikkati aynı zamanda suyun kapların dibindeki ağızlardan akışına odaklanmıştır. İçi su dolu silindirik alanın iki parçadan oluştuğunu kabul edip bu parçaların kısım kısım hareket analizini yapmıştır. Bu ikiye bölümden çıkan hiperboloid katmanın yatay katmanının her an hareket halindeyken, suyun kalanının durma halinde olduğunu varsayıp ortadaki kısmın bir tür katarakt halinde olduğunu savlamıştır. Kuramının tahmin ettiği dökülen su miktarı deneylerle karşılaştırıldığında, Newton ağızdan dökülen suyun hızının suyun rezervuardaki yüksekliğinin yarısından dökülen bir cismin hızına eşit olduğunu hesaplamıştır. Fakat bu hesap suyun rezervuardaki yüksekliğine yükseldiği şeklindeki gözlemle çeliştiğinden Newton, Principia’nın ikinci versiyonunda değiştirmeler yapmıştır. Sıvının oluğunda sıkışmalar keşfetmiş ve açıklık çapı kadar bir mesafede oluğun yarıya kadar sıkıştığını gözlemlemiştir.[4]
Dalgalar
Sir Isaac Newton dalgaların hareketini inceleyen ilk bilim insanı olmuştur.[4]
Daniel Bernoulli
1738 yılında Daniel Bernoulli, "Hydrodynamica seu de viribus et motibus fluidorum commentarii" isimli kitabını yayınlamıştır. Bir kap içerisindeki bir delikten boşalan sıvının her zaman yatay kaldığını; bu şekilde sıvı kütlesi sonsuz sayıda yatay katmana bölündüğünde, her katmanın birbirine bitişik kaldığını ve akış esnasında katmandaki her noktanın dikey şekilde ve genişlikle ters orantılı bir hızla alçaldığını not etmiştir. Bu şekilde boşalan suyun hareketini katmanlar üzerinden formüle edebilmiştir. Colin Maclaurin ve Johann Bernoulli, bundan daha doğrudan yöntemler ile aynı probleme yaklaştıklarından, bu çözümü yeterli bulmamışlardır. Jean le Rond d'Alembert, Bernouilli'nin teorisine en çok karşı çıkanlardandır. Jakob Bernouilli, sarkaç kuramını genelleştirirken çok basit ve genel bir dinamik prensibi keşfederek, bu cisimlerin hareket yasalarını bu cisimlerin denge halindeki hareketine indirgemeyi başarmıştır. Daniel Bernouilli ile aynı ön kabulleri kullansa da daha detaylı bir kalkülüs kullanmıştır. Her anda, katmanın hareketini bir önceki andaki hareket ve kaybettiği hareketin bir bileşimi olarak görerek kuramlaştırırken, bu hareketi biçimlendirecek hareket denklemlerini bulmak d’Almbert’e kaldı. d'Alembert'in iki prensibine göre - dengedeki sıvı kütlesi olarak ele alınmış dikdörtgensel bir kanalın kendisi dengededir ve sıvının bir kısmı, bir yerden diğerine geçerken sıvı sıkıştırılamaz ise aynı hacmi korur ya da sıvı elastik ise genleşir. Bu önemli metot Leonhard Euler tarafından da kullanılmıştır. Akışkanlar dinamiğinde Bernoulli ilkesi, sürtünmesiz bir akış boyunca, hızda gerçekleşen bir artışın aynı anda ya basınçta ya da akışkanın potansiyel enerjisinde azalmaya neden olduğunu ifade eder. Bernoulli ilkesi, adını Hollanda-İsviçre kökenli matematikçi Daniel Bernoulli'den almıştır. Bernoulli bu ilkesini 1738 yılında Hydrodynamica adlı kitabında yayınlamıştır.[4]
Bazen Bernoulli ilkesi olarak da geçen bu ile farklı türlerde akışkan debileri üzerinde uygulanabilir. Aslında farklı türlerde akımlar için farklı Bernoulli denklemleri vardır. Bernoulli ilkesinin en basit hali sıkıştırılamaz akımlar (örn. çoğu sıvı akımlar) ve düşük Mach sayısında hareket eden sıkıştırılabilir akımlar (örn. gazlar) için geçerlidir. Bernoulli ilkesi, enerjinin korunumu yasasından çıkarılabilir. Buna göre sabit bir akımda, bir yolda hareket eden akışkanın sahip olduğu tüm mekanik enerjilerin toplamı yine bu yol üzerindeki her noktada eşittir. Bu ifade kinetik ve potansiyel enerji toplamlarının sabit olduğunu ifade eder. Bu yüzden akışkanın hızındaki herhangi bir artış, akışkanın dinamik basıncını ve kinetik enerjisini orantılı olarak artırırken statik basıncını ve potansiyel enerjisini düşürür.
Leonhard Euler
Akışkanların hareketine ilişkin soruların cevaplanması Leonhard Euler’in kısmi diferansiyel denklemleri sayesinde gerçekleşmiştir. Bu kalkülüs suyun hareketine önce d’Alembert tarafından uyarlanmış olup onun ve Euler’in akışkan teorisini belirli bir hipotez olmadan formüle etmesine yardımcı olmuştur. Euler, şimdi Bernoulli ilkesi olarak bilinen bağıntıları ilk geliştirendir. Açık kanal akışları, boru akışları, dalgalar, türbinler ve gemi sürüklenme katsayıları üzerinde Antonie de Chezy (1718-1789), Henri Pitot (1695-1771), Wilhelm Eduard Weber (1804-1891), James Bicheno Françis (1815- 1892), Jean Louis Marie Poiseouille (1799-1869) yaptıkları deneysel çalışmalarla akışkanlar mekaniğinin geliştirilmesinde önemli katkılarda bulunmuşlardır.[4]
Pierre Louis Georges du Buat
Hidrodinamik biliminde en başarılı bilim insanlarından biri Pierre Louis Georges du Buat’tır (1734-1809). Abbe Charles Bossut’nun izlerinden giderek, 1786'da tamamen deneyler üzerine kurulu akışkan hareketi kuramını yayınlamıştır. Buat, su ideal bir akışkan olsa ve üzerinde aktığı kanallar sonsuz şekilde pürüzsüz olsa, hareketi sürekli olarak ivmelenir diyerek bu hareketi eğimli bir düzlemden kaymakta olan cisimlere benzetmiştir. Fakat nehirlerin hareketi ivmelenmediğinden, suyun viskozitesi ve kanalın sürtünmesi ivmelenme kuvvetine eşit olmalı. Bu şekilde Buat, suyun bir kanalda akarken ivmelenmesine ilişkin kuvvetin karşılaştığı sürtünme kuvvetleri toplamına eşit olması gerektiğini fark etmiştir.[4]
On dokuzuncu yüzyıl
Hermann von Helmholtz
1858 yılında Hermann von Helmholtz’un önemli makalesi "Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen”, Journal für die reine und angewandte Mathematik dergisinin 55. sayısının 22-55. sayfaları arasında yayınlandı. Bu makale o kadar önemli bir hüviyetteydi ki, birkaç yıl sonra P. G. Tait, bu makalenin “On integrals of the hydrodynamical equations which express vortex motion” adında bir İngilizce çevirisini Philosophical Magazine’in 33. sayısının 485-512. sayfaları için kaleme aldı (1867). Makalesinde Helmholtz, vorteks hareketinin üç yasasını, bugün akışkan mekaniği ders kitaplarında bulunduğu şekilde ortaya koydu. Bu çalışma akışkanlar dinamiğinde ve genel olarak bilim içerisinde vortisitenin önemini ortaya koymuş oldu. Sonraki yüzyılda vorteks dinamiği akışkanlar dinamiğinin bir alt başlığı olarak önem kazandı.
H. Lamb’in meşhur Hidrodinamik isimli kitabı (1932) vortisiteye ve Vorteks Dinamiğini,[15] G. K. Batchelor’ın Akışkanlar Dinamiği'ne Giriş[16] (1967) gibi bir bölüm ayırmaktadır. Zamanla bu konu üzerine bütün kitaplar yazılmaya başlandı. H. Poincare 1983'te, H. Villat 1930'da, C. Truesdell 1954'te, P. G. Saffman 1992'de bu konu üzerine önemli kitaplar yazdılar. Başlarda konferansların bir alt başlığı dahilinde girdap hareketi, vorteks dinamiği, vorteks akışı gibi konular tartışılsa da, daha sonra bütünüyle bunun üzerine olan toplantılar yapılmaya başlandı. Helmholtz'un çalışmalarının atmosferik ve okyanus akışlarını da içerecek şekilden, mühendisliğin ve uygulamalı bilimlerin bütün alanlarına yaygınlaşması gerçekleşmedi. Modern akışkanlar dinamiğinde vorteks dinamiğinin akış fenomeni bağlamındaki rolü sağlam bir şekilde açıklanmıştır. Girdap (Vortex) olayları çeşitli isimler alıp popüler basında fırtınalar, tornadolar, sel baskınları, uçak vortisleri, buhar halkaları, su altı baloncuk hava ringleri, gemi pervanelerindeki kavitasyon vortisleri gibi bağlamlar dahilinde yer almıştır.
Gaspard Riche de Prony
Akan suyun teorisi, 1755 ve 1839 yılları arasında yaşamış Gaspard Riche de Prony’nin teorileriyle gelişmiştir. Prony, bu alanda yapılmış en iyi deneylerin bir araya getirilmesiyle, genel bir formül kurarak akan suyun hızı için basit bir ifade ortaya koyabilmiştir.[4]
Johann Albert Eytelwein
J. A. Eytelwein 1801'de yayınlanmış Handbuch der Mechanik und der Hydraulik isimli kitabında, borulardan su akışını, jetlerin hareketini ve uçaklara olan etkilerini çalışmış olup teorik olarak su çarkının en verimli hareketinin suyun akış hızının yarısına sahip bir çevre ile olacağını göstermiştir.[4]
Jean Nicolas Pierre Hachette ve diğerleri
J. N. P. Hachette 1816 yılında akışkanların püskürmesine ilişkin deney sonuçları içeren anılarını yayınladı. Amacı akışkanın sıkışmış bölümlerini araştırmaktı. P. P. Boileau (1811-1891) bu sonuçları kullanıp kendi deneylerini yaptı (Traité de la mesure des eaux courantes, Paris, 1854). K. R. Bornemann bu sonuçları kullanarak kendi formülasyonunu oluşturdu (Civil Ingenieur, 1880). Julius Weisbach (1806-1871) ise aynı konuda kendi deneysel araştırmalarını gerçekleştirdi. J. B. Francis'in deneyleri (Lowell Hydraulic Experiments, Boston, Mass., 1855) bu genel formülasyondan sapmalar ortaya koydu. Suyun borular ve kanallar içerisindeki hareketi hakkında çok detaylı bir çalışma yapan H. G. P. Darcy’nin çalışmaları (1803-1858), daha sonra H. Bazin tarafından devam ettirildi.[4]
Andreas Rudolf Harlacher ve diğerleri
Alman mühendisleri de nehirlerdeki akışa özel olarak özen göstererek, bu konuda birçok çalışma yaptılar. A. R. Harlacher Mississippi nehrinden alınmış ölçümler ile Ganj kanalından alınan verileri kullandı.[17] Suyun sürtünmesi daha önce Coulomb tarafından çalışılmış olup daha yüksek hızlar için William Froude (1810-1879) tarafından genişletmiş olup gemilerin direncinin hesaplamasında kullanılmıştır.[4]
Yirminci yüzyıl
Ludwig Prandtl
1904 yılında Alman bilim adamı Ludwig Prandtl sınır tabakası teorisine öncülük etti. Küçük viskoziteli akışkanların, katı yüzeylerin ve arayüzeylerin yakınında ince bir viskoz katmana (sınır katmanı) ve Bernoulli ilkesinin ve Euler denklemlerinin geçerli olduğu bir dış katmana bölünebileceğini belirtti.[18]
Girdap dinamiklerindeki gelişmeler
Vorteks dinamiğindeki gelişmeler Vorteks dinamiği önemli bilimsel konferans, çalıştay ve sempozyumlarda yer alan, akışkanlar dinamiğinin önemli bir alt başlığıdır. Vorteks dinamiği tarihinde dikkat çeken bir sapma Lord Kelvin olarak da bilinen William Thomson tarafından önerilen vorteks atom teorisi ile gerçekleşmiştir. Kelvin'in teorisine göre atomlar eter denilen alanda vorteks hareketi yapıyor şekilde temsil edilebilirlerdi. Kuantum teorisinden onlarca yıl önce ortaya konan bu teori, fikri ortaya atanın bilimsel çevrelerdeki kredibilitesinden dolayı önemli ölçülerde dikkat çekti. Bu doğrultuda, bu teoriyi tamamlamak için birçok çalışma yapıldı.
P. G. Tait bugün çizge kuramının, topolojinin temeli kabul edilen düğüm sayımı işlemini bu teoriye paralel olarak yapmış olsa da, Kelvin’in teorisi zamanın testine uzun vadede dayanamadı. Bununla beraber, bu çaba doğrultusunda elde edilen birçok veri bugün vorteks dinamiğinin gelişmesine önemli katkıda bulundu. Kelvin’in kendisi dolaşım teorisini ortaya attı ve bir materyal kontoru etrafındaki viskoz olmayan sıvı dolaşımının korunacağını matematiksel olarak ispat etti. Einstein tarafından Kelvin’in en önemli sonuçlarından biri olarak taltif edilen bu sonuç, akışkan dinamiği ile topoloji arasındaki ilk bağlantılardan biri kurmuş oldu.
Vorteks dinamiğinin tarihi keşifler kadar önemli keşiflerin tekrar keşfiyle doludur, zira çok önceden elde edilmiş sonuçlar keşiflerinden sonra tekrar keşfedilene kadar tamamen unutulmuşlardır. Örneğin üç nokta vorteksi problemini 1877 yılında yazdığı teziyle genç İsviçreli matematikçi Walter Gröbli çözmüş olsa da, Gröbli'nin çözümü 1970'lere kadar unutulmuş olup ancak 1979 yılında, kaos teorisi bağlamında gün yüzüne çıkmıştır. 1960'ların ortasından itibaren Arms, Hama, Betchov ve diğerlerinin çalışmalarıyla popülerlik kazanan, üç boyutlu vorteks filament hareketindeki “lokalize indüksiyon yaklaşımı”, esasında 20. yüzyılın başında, kendisi de T. Levi-Civita’nın öğrencisi olan, yetenekli İtalyan matematikçi Da Rios tarafından ortaya konmuştur. 1972 yılında H. Hasimoto, Da Rios'un “içsel denklemleri”ni kullanarak (daha sonra R. Betchov tarafından bağımsız olarak ortaya konmuş), bu yaklaşım dahilinde vorteks filament hareketinin doğrusal olmayan Schrödinger denklemine bağlanabileceğini göndermiştir. Bu şekilde, bu problem vorteks filamentlerin büyük genlikli döngü dalgalarını destekleyebileceği görüldüğünden, “modern bilim”in bir parçası haline gelmiş oldu.
Daha fazla bilgi için
Donald F. Young, Bruce R. Munson, Theodore H. Okiishi, Wade W. Huebsch (2019). Akışkanlar Mekaniğine Giriş / A Brief Introduction to Fluid Mechanics. Yücel, Nuri & Türkoğlu, Haşmet tarafından çevrildi. Nobel Akademik Yayıncılık. ISBN 978-605-133-443-1
Not
- ^ Arap bilim adamları, bir dizi matematiksel yöntem kullanarak (yalnızca antik oranlar teorisinden ve sonsuz küçük tekniklerden miras alınanları değil, aynı zamanda çağdaş cebir ve ince hesaplama tekniklerini de kullanarak), statiği yeni, daha yüksek bir seviyeye yükselttiler. Arşimet'in ağırlık merkezi teorisindeki klasik sonuçları genelleştirildi ve üç boyutlu cisimlere uygulandı, ağır kaldıraç teorisi kuruldu ve 'yerçekimi bilimi' yaratıldı ve daha sonra ortaçağ Avrupa'sında daha da geliştirildi. Statik olgusu dinamik yaklaşım kullanılarak incelendi, böylece iki eğilimin (statik ve dinamik) tek bir bilim olan mekanik kapsamında birbiriyle ilişkili olduğu ortaya çıktı. Dinamik yaklaşımın Arşimet hidrostatiği ile birleşimi, bilimde ortaçağ hidrodinamiği olarak adlandırılabilecek bir yön doğurdu. Arşimet statiği, özgül ağırlık biliminin temellerini oluşturmanın temelini oluşturdu. Özgül ağırlığın belirlenmesi için özellikle denge ve tartım teorisine dayanan çok sayıda ince deneysel yöntem geliştirilmiştir. El-Biruni ve el-Hazini'nin klasik eserleri, ortaçağ biliminde deneysel yöntemlerin uygulanmasının başlangıcı olarak kabul edilebilir. Arap statiği dünya biliminin ilerlemesinde önemli bir bağlantıydı. Ortaçağ Avrupa'sında klasik mekaniğin tarihöncesinde önemli bir rol oynadı. O olmasaydı klasik mekanik muhtemelen yaratılamazdı.
Kaynakça
- ^ Gunther Garbrecht (1987). Hydraulics and Hydraulic Research: A Historical Review (İngilizce). A A Balkema Publishers. ISBN 978-9061916215.
- ^ Colin A. Ronan (1982). Science and civilization in china (İngilizce). Cambridge University Press. s. 336. ISBN 978-0521235822.
archive.org
- ^ Carroll, Bradley W. "Archimedes' Principle". Weber State University. 17 Mayıs 2015 tarihinde kaynağından arşivlendi. Erişim tarihi: 23 Temmuz 2007.
- ^ a b c d e f g h i j k l m n o p Alfred George Greenhill (1911). Hugh Chisholm (Ed.). Hydromechanics. 1911 Encyclopædia Britannica (İngilizce). 14. Cambridge University Press. ss. 115-116. 3 Haziran 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 5 Aralık 2023.
- ^ Ahmad S. Saidan, Roshdi Rashed, Boris A. Rosenfeld, Adolf P. Youschkevitch, Marie-Therese Debarnot, Andre Allard, Jean-Claude Chabrier, Mariam Rozhanskaya, Gul A. Russell, David C. Lindberg (1996). Roshdi Rashed (Ed.). Statics Mariam Rozhanskaya (in collaboration with /. S. Levinova) (PDF). Encyclopedia of the History of Arabic Science (İngilizce). 2. Routledge. ss. 614-642. 18 Nisan 2023 tarihinde kaynağından arşivlendi (PDF). Erişim tarihi: 5 Aralık 2023.
- ^ Clagett, Marshall (1959). The science of mechanics in the middle ages (İngilizce). Univ. of Wisc. Pr. s. 64. ISBN 978-0-299-01900-6.
- ^ Robert E. Hall (1973). Al-Biruni (İngilizce). VII. Dictionary of Scientific Biography. s. 336.
- ^ a b c Ahmad Y. al-Hassan. "İSLAM TEKNOLOJİSİNİN BATI'YA TRANSFERİ BÖLÜM II: İSLAM MÜHENDİSLİĞİNİN AKTARIMI" (İngilizce). history-science-technology.com. 18 Şubat 2008 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Aralık 2023.
- ^ Adamy, J.; Flemming, A. (1 Kasım 2004). "Soft variable-structure controls: a survey". Automatica. 40 (11): 1821-1844. doi:10.1016/j.automatica.2004.05.017. ISSN 0005-1098.
- ^ a b c Otto Mayr (15 Temmuz 1975). Geri Besleme Kontrolünün Kökenleri (İngilizce). The MIT Press.
- ^ a b c d Donald R. Hill (Mayıs 1991). Carol L. Moberg, Zanvil A. Cohn, George Brimhall, Carver Mead, Misha A. Mahowald, Norbert Hirschhorn, William B. Greenough, Patrick Cunningham, Frank Wilczek, Elizabeth Corcoran, Donald R. Hill (Ed.). "Ortaçağ Yakın Doğu'da Makine Mühendisliği" (İngilizce). 264 (5). Scientific American. ss. 64-69, 143, 150-152. 25 Aralık 2007 tarihinde kaynağından arşivlendi.
- ^ a b Banū Mūsá; Hill, Donald Routledge (1979). The book of ingenious devices: Kitāb al-ḥiyal (İngilizce). Dordrecht: D. Reidel Pub. Co. ISBN 978-90-277-0833-5.
- ^ "Antik Keşifler, Bölüm 12: Doğunun Makineleri" (İngilizce). History Channel. 27 Eylül 2022 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Aralık 2023.
- ^ Donald Routledge Hill. Roshdi Rashed (Ed.). "Arap Bilim Tarihi Ansiklopedisi" (İngilizce). Cilt 2. Routledge. ss. 751-795. 28 Kasım 2023 tarihinde kaynağından arşivlendi. Erişim tarihi: 9 Aralık 2023.
- ^ "Vortex Dynamics" (İngilizce). Cambridge. 14 Mart 2007 tarihinde kaynağından arşivlendi.
- ^ "Cambridge Mathematical Library" (İngilizce). Cambridge. 3 Mayıs 2008 tarihinde kaynağından arşivlendi.
- ^ Leveson Francis Vernon-Harcourt (10 Ekim 2018). Rivers and Canals: Rivers (İngilizce). 1. Franklin Classics. ISBN 978-0342171125. OCLC 967596679.
- ^ White, Frank M. (2003). Fluid mechanics. 5. ed., International ed (İngilizce). New York London: McGraw-Hill. ISBN 978-0-07-119911-7.


















