Ackermann işlevi
Ackermann işlevi, ismini Wilhelm Ackermann'dan alan oldukça hızlı büyüyen bir işlevdir. Özyinelemeli olup işlevlerin göreceli olarak en basitidir. Özellikle karmaşıklık çözümlemesinde kullanılır.
kümesinde Tanımı aşağıdaki gibidir:
Ackermann işlevi, ismini Wilhelm Ackermann'dan alan oldukça hızlı büyüyen bir işlevdir. Özyinelemeli olup işlevlerin göreceli olarak en basitidir. Özellikle karmaşıklık çözümlemesinde kullanılır.



Tam sayılar, sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar ve bunların negatif değerlerinden oluşan negatif sayılardan oluşan sayı kümesidir.

Grup teorisi veya Grup kuramı, simetrileri inceleyen matematik dalıdır. Simetri kuramı olarak da adlandırılabilir. Bir nesnenin simetrileri ile kast edilen, nesneye uygulandığında nesneye hiçbir etki olmamış gibi sonuç veren dönüşümlerdir. Her nesnenin en az bir simetrisi vardır: hiçbir şey yapmadan olduğu gibi bırakma dönüşümü. Bahsettiğimiz dönüşümlerin tersleri de vardır ve aradığımız özellikleri sağlarlar. Son olarak da dönüşümlerin art arda yapılması, birleşimli bir işlemdir. Bu üç koşula sırasıyla birim elemana sahip olma, elemenların tersi olma ve grup işleminin birleşmeli olması denir. Bu kavramların matematikte soyutlanması, üzerinde tersinebilir ve bileşme özelliğine sahip ikili bir işlemin tanımlı olduğu kümeler ile yapılır. Daha detaylı açıklamak gerekirse, grup nesnesi bir küme G ve onun üzerinde tanımlı bir 

Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.
Fonksiyon, matematikte değişken sayıları girdi olarak kabul edip bunlardan bir çıktı sayısı oluşmasını sağlayan kurallardır. Fonksiyon, 17. yüzyılda matematiğin kavramlarından biri olmuştur. Fizik, mühendislik, mimarlık ve birçok alanda kullanılmaktadır. Galile, Kepler ve Newton hareketlerin araştırılmasında, zaman ve mesafe arasındaki durumu incelemek için fonksiyonlardan faydalanmıştır. Dört işlemden sonra gelen bir işlem türüdür.
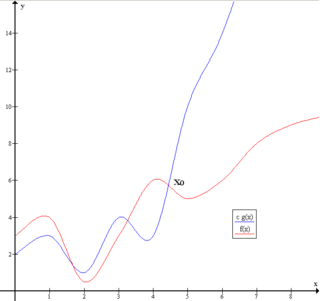
Büyük O (Big-Oh) gösterimi matematiksel bir gösterim olup işlevlerin (fonksiyonların) asimptotik davranışlarını tarif etmek için kullanılır. Bir işlevin büyümesinin asimptotik üst sınırını daha basit başka bir işlev cinsinden tanımlanması demektir. İki temel uygulama alanı vardır: matematik alanında genellikle kırpılmış bir sonsuz serinin kalan terimini karakterize etmek için kullanılır; bilgisayar bilimlerinde ise algoritmaların bilgi işlemsel karmaşıklığının çözümlemesi için kullanılır.

Rasyonel sayılar, iki tam sayı arasındaki oranı temsil eden, bir pay p ve sıfırdan farklı bir payda q olmak üzere, bir bölme işlemi veya kesir formunda ifade edilebilen sayıları tanımlar. Örneğin, 


Kısmi türev çok değişkenli bir işlevin(fonksiyon), sadece ilgili değişkeni sabit değilken alınan türevdir. Bu tarz türevleri içeren denklemlere kısmi diferansiyel denklem denir.

Serbest veya bağlı bir parçacığa enerjisinden büyük bir potansiyel engelinin uygulanması sonra engelin kaldırılması durumunda parçacığın sızabilme, diğer bir deyişle engelin içinden geçebilme olayıdır. Makro düzeyde bahsedilecek olunursa insanın duvarın içinden geçebilmesi durumu olarak tasvir edilebilir. Serbest parçacık için problemi tek boyutta ele alırsak, parçacığa etki eden potansiyel matematiksel olarak:
Potansiyel kuyusu, bir parçacığın bağlı olması durumunu modelleyen sistemdir. Tek boyutta uygulanan potansiyel,
Kronecker deltası veya Kronecker delta fonksiyonu, Leopold Kronecker tarafından tanımladığından onun adını almıştır.

Halka, matematikte cebirin temel yapılarından biridir ve soyut cebirde tam sayıların soyutlamasıdır. Bu yapıyı işleyen dala halka kuramı denir. Halkalar diğer bir temel yapı olan grupların üzerine inşa edilir. Her halka, aynı zamanda değişmeli bir gruptur, ama bir halkadan daha fazla özelliği sağlaması istenir. Örneğin halkada grup işlemine ek olarak ikinci bir işlem daha vardır. Halkalara örnek olarak tam sayılar, modülo n sayılar, polinomlar ya da karmaşık sayılar verilebilir.

HSL ve HSV, 1970'lerde bilgisayar grafikleri araştırmacıları tarafından insan vizyonunun renk oluşturma özelliklerini algılama biçimiyle daha yakından uyumlu olması için tasarlanan RGB renk modelinin alternatif temsilleridir. Bu modellerde, her renk tonunun renkleri, alttan siyahtan üste beyaz arasında değişen nötr renklerin merkezi ekseni etrafında radyal bir dilim halinde düzenlenir. HSV temsili, farklı renkteki boyaların birbirine karışma şeklini, parlak renkli boyaların çeşitli renk tonlarını andıran doygunluk boyutu ve değişen miktarlarda siyah veya beyaz boya ile bu boyaların karışımına benzeyen değer boyutu modellenir. HSL modeli, Doğal Renk Sistemi (NCS) veya Munsell renk sistemi gibi daha algısal renk modellerine benzemeye çalışır ve Doygun renkleri 1⁄2 parlaklık değerinde bir dairenin etrafına yerleştirir, burada 0 veya 1 parlaklık değeri tamamen siyah veya beyazı temsil eder.
Matematikte karmaşık sayı, bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:


Özyineleme ya da yinelge, en genel anlamıyla bir yapının yinelenmesidir. Özellikle matematik ve bilgisayar biliminde kullanılır. Bu yapılara yinelgen yapılar denir. Yinelgen bir yapı eğer kendine gönderme yapma özelliğiyle yinelgen ise bu tür yapılara özgöndergeli ya da kendine-göndergeli yapılar denir.
Cisim, halka ve grup gibi soyut bir cebirsel yapıdır. Kabaca, elemanları arasında toplama, çıkarma, çarpma ve bölme yapılabilen ve bu işlemlerde sayılardan alışık olduğumuz temel aritmetik kurallarının geçerli olduğu bir küme olarak tanımlanabilir.

Olasılık kuramı bilim dalında bir olasılık kütle fonksiyonu bir ayrık rassal değişkenin olasılığının tıpatıp belli bir değere eşit olduğunu gösteren bir fonksiyondur. Olasılık kütle fonksiyonu, olasılık yoğunluk fonksiyonundan farklıdır; çünkü olasılık yoğunluk fonksiyonu yalnızca sürekli rassal değişkenler için tanımlanmış olup doğrudan doğruya olasılık değerini vermezler. Olasılık yoğunluk fonksiyonunun bir belli değer aralığı için integrali alınırsa bu rassal değişkenin belirlenen değer aralığı için olasılığını verir.
Hiperişlem, matematik'te aritmetik işlemlerin sonsuz dizisidir. Ardılın birli işlemi, ardından toplama, çarpma ve üs almanın iki işlemiyle devam eden ve ardından ikili işlemlerin ötesine geçerek serilerle ilerleyen bir işlemdir. Üstelden sonraki işlemler için bu dizinin n. elemanı Reuben Goodstein tarafından adlandırıldı. n Yunan önekinden sonra -syon son eki kullanılarak elde edilir ve Knuth yukarı ok gösterimindeki n-2 okları kullanılarak yazılabilir. Her hiperişlem, önceki terimlerin yinelemesi olarak tanımlanır. Ackermann işlevi, Knuth yukarı ok gösterimini kullanarak şöyle yinelenebilir:

Lineer cebirde, doğrusal dönüşümler matrislerle temsil edilebilir. 







Lineer cebirde, özdeğer ayrışımı ya da eigen ayrışımı, bir matrisin özdeğerleri ve özvektörleri cinsinden ifade edilen daha basit matrislere ayrıştırılmasıdır. Sadece kare matrisler özdeğerlerine ayrıştırılabilir.