Algoritma, belli bir problemi çözmek veya belirli bir amaca ulaşmak için tasarlanan yol. Matematikte ve bilgisayar biliminde bir işi yapmak için tanımlanan, bir başlangıç durumundan başladığında, açıkça belirlenmiş bir son durumunda sonlanan, sonlu işlemler kümesidir. Genellikle bilgisayar programlamada kullanılır ve tüm programlama dillerinin temeli algoritmaya dayanır. Aynı zamanda algoritma tek bir problemi çözecek davranışın, temel işleri yapan komutların veya deyimlerin adım adım ortaya konulmasıdır ve bu adımların sıralamasına dikkat edilmelidir. Bir problem çözülürken algoritmik ve sezgisel (herustic) olmak üzere iki yaklaşım vardır. Algoritmik yaklaşımda da çözüm için olası yöntemlerden en uygun olan seçilir ve yapılması gerekenler adım adım ortaya konulur. Algoritmayı belirtmek için; metinsel olarak düz ifade ve akış diyagramı olmak üzere 2 yöntem kullanılır. Algoritmalar bir programlama dili vasıtasıyla bilgisayarlar tarafından işletilebilirler.

Yapay sinir ağları (YSA), insan beyninin bilgi işleme tekniğinden esinlenerek geliştirilmiş bir bilgi işlem teknolojisidir. YSA ile basit biyolojik sinir sisteminin çalışma şekli taklit edilir. Yani biyolojik nöron hücrelerinin ve bu hücrelerin birbirleri ile arasında kurduğu sinaptik bağın dijital olarak modellenmesidir. Nöronlar çeşitli şekillerde birbirlerine bağlanarak ağlar oluştururlar. Bu ağlar öğrenme, hafızaya alma ve veriler arasındaki ilişkiyi ortaya çıkarma kapasitesine sahiptirler. Diğer bir ifadeyle, YSA'lar, normalde bir insanın düşünme ve gözlemlemeye yönelik doğal yeteneklerini gerektiren problemlere çözüm üretmektedir. Bir insanın, düşünme ve gözlemleme yeteneklerini gerektiren problemlere yönelik çözümler üretebilmesinin temel sebebi ise insan beyninin ve dolayısıyla insanın sahip olduğu yaşayarak veya deneyerek öğrenme yeteneğidir.
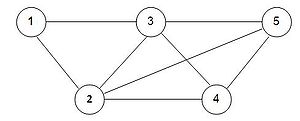
Seyyar satıcı problemi yöneylem araştırması ve teorik bilgisayar bilimi alanlarında incelenen bir "kombinatorik optimizasyon" problemidir.
Paralel hesaplama ya da Koşut hesaplama, aynı görevin, sonuçları daha hızlı elde etmek için çoklu işlemcilerde eş zamanlı olarak işletilmesidir. Bu fikir, problemlerin çözümünün ufak görev parçalarına bölünmesi ve bunların eş zamanlı olarak koordine edilmesine dayanır. Paralel hesaplama ile performans artar, büyük sorunlar daha az sürede çözülür ve bilimdeki gelişmeler paralel hesaplamaya gereksinim duyar.
Veri yapısı, bilgisayar ortamında verilerin etkin olarak saklanması ve işlenmesi için kullanılan yapı.

Genetik algoritmalar, doğada gözlemlenen evrimsel mekanizmalara benzer mekanizmalar kullanarak çalışan eniyileştirme yöntemidir. Çok boyutlu uzayda belirli bir maliyet fonksiyonuna göre en iyileştirme amacıyla iterasyonlar yapan ve her iterasyonda en iyi sonucu üreten kromozomun hayatta kalması prensibine dayanan en iyi çözümü arama yöntemidir.
Matematikte matematiksel programlama, eniyileme ya da optimizasyon terimi; bir gerçel fonksiyonu minimize ya da maksimize etmek amacı ile gerçek ya da tam sayı değerlerini tanımlı bir aralıkta seçip fonksiyona yerleştirerek sistematik olarak bir problemi incelemek ya da çözmek işlemlerini ifade eder. Örneğin bu problem şöyle olabilir:

Yöneylem araştırması, belirli kısıtların olduğu bir durumda, belirli bir amaca yönelik en uygun çözümün bulunması için geliştirilmiş bir yöntem.

Sırt çantası problemi bir klasik yöneylem araştırması ve matematiksel olarak "kombinatorik optimizasyon" problemidir. Çözüm algoritması bakımından sırt çantası problemi en ünlü NP-hard problemleri arasındadır.
Matematik biliminde, özellikle yöneylem araştırması uygulamalı dalında, doğrusal programlama problemleri bir doğrusal amaç fonksiyonunun doğrusal eşitlik ve/veya eşitsizlik kısıtlamalarını sağlayacak şekilde optimizasyon yapılmasıdır. Bir optimizasyon modeli eğer sürekli değişkenlere ve tek bir doğrusal amaç fonksiyonuna sahipse ve tüm kısıtlamaları doğrusal eşitlik veya eşitsizliklerden oluşuyorsa, doğrusal (lineer) program olarak adlandırılır. Başka bir deyişle, modelin tek-amaçlı fonksiyonu ve tüm kısıtlamaları, süreklilik gösteren karar değişkenlerinin ağırlıklı toplamlarından oluşmalıdır.

Sayısal analiz, diğer adıyla nümerik analiz veya sayısal çözümleme, matematiksel analiz problemlerinin yaklaşık çözümlerinde kullanılan algoritmaları inceler. Bu nedenle birçok mühendislik dalı ve doğa bilimlerinde önem arz eden sayısal analiz, bilimsel hesaplama bilimi olarak da kabul edilebilir. Bilgisayarın işlem kapasitesinin artması ile gündelik hayatta ortaya çıkan birçok sistemin matematiksel modellenmesi mümkün olmuş ve sayısal analiz algoritmaları burada ön plana çıkmıştır. 21. yüzyıldan itibaren bilimsel hesaplama yöntemleri mühendislik ve doğa bilimleri ile sınırlı kalmamış ve sosyal bilimler ile işletme gibi alanları da etkilemiştir. Sayısal analizin alt başlıklarına adi diferansiyel denklemlerin yaklaşık çözümleri ve özellikle veri biliminde önem taşıyan sayısal lineer cebir ile optimizasyon örnek gösterilebilir.

Toyota Coaster, Toyota Motor Corporation tarafından üretilen bir midibüs modelidir.

Hesaplamalı fizik, fizik sorunlarını çözebilmek için sayısal algoritmaların üretilmesi ve gerçeklenmesini içerir. Genelde kuramsal fizikin bir alt dalı olarak değerlendirilir ancak bazen de kuramsal ve deneysel fizik arasında orta bir dal olarak da düşünülür.
Sayı teorisinde, asal çarpanlara ayırma bir bileşik sayının, çarpıldıklarında yine aynı sayıyı verecek şekilde, bir ve kendisi dışındaki bölenlerine ayrılmasıdır.
Matematikte, özellikle soyut cebir ve uygulamalarında, ayrık logaritma, genel logaritmanın grup kuramındaki karşılığıdır. Genel olarak bakıldığında, loga(b) ifadesi, ax = b ifadesinin gerçel sayılar kümesi içindeki çözümlerine karşılık gelir. Benzer olarak, g ve h sonlu devirli grup G'nin elemanları olduğunda, gx = h ifadesinin çözümü olan x sonuçlarına h'nin g tabanındaki ayrık logaritması denir.

K-ortalama kümeleme ya da K-means kümeleme yöntemi N adet veri nesnesinden oluşan bir veri kümesini giriş parametresi olarak verilen K adet kümeye bölümlemektir. Amaç, gerçekleştirilen bölümleme işlemi sonunda elde edilen kümelerin, küme içi benzerliklerinin maksimum ve kümeler arası benzerliklerinin ise minimum olmasını sağlamaktır.
Bilgisayar bilimi, matematik, ekonomi ve biyoinformatikte dinamik programlama karmaşık bir problemi tekrarlanan alt problemlere bölerek, her bir alt problemi yalnız bir kere çözüp daha sonra bu çözümü kaydederek karmaşık problemin çözümünde kullanma yöntemidir. Bir alt problem çözüldükten sonra tekrar çözülmesi gerektiğinde daha önce kaydedilen çözüm kullanılarak zaman kazanılır, ancak alt problemlerin kaydedileceği daha fazla alana gereksinim duyulur. Yani dinamik programlama algoritmaları alandan ödün verilerek zamandan kazanılmasını sağlar. Dinamik programlama algoritmaları optimizasyon problemlerinin çözümünde yaygın olarak kullanılır.

Analiz, karmaşık bir konuyu veya maddeyi daha iyi anlamak için daha küçük parçalara ayırma sürecidir. Teknik, matematik ve mantık çalışmalarında Aristoteles'ten önce uygulanmıştır.
Tepe Tırmanma Algoritması, yapay zeka alanındaki matematiksel optimizasyon problemleri için kullanılan sezgisel bir algoritmadır. Çok sayıda verinin girilmesi ve iyi bir sezgisel fonksiyon verildiğinde, probleme yeterince iyi bir çözüm bulmaya çalışmaktadır. Bilgisayar bilimlerinde aktif olarak kullanılmakta olan arama algoritmalarından birisidir. İki boyutlu bir grafikte en düşük noktaları arama esnasında yapmış olduğu hareket tepe tırmanmaya benzemesinden dolayı bu isimi almıştır.
Literatürde ilk defa Hakimi tarafından tanıtılan ve p-medyan problemi adı verilen bu problem, yer seçim problemleri kategorisinde bulunan bir kombinatoryal optimizasyon problemidir. 1964 yılında Hakimi tarafından yapılan çalışmada, telekomünikasyon şebekesi üzerindeki merkez noktalarına ve yol üzerindeki polis merkezlerine en uygun yerleri belirlemek amacıyla bir model geliştirilmiştir.