Açıortay teoremi

Geometride açıortay teoremi, bir üçgenin kenarının karşı açıyı ikiye bölen bir çizgiyle bölündüğü iki parçanın göreli uzunluklarıyla ilgilidir. Göreli uzunluklarını, üçgenin diğer iki kenarının göreli uzunluklarına eşitler.
Teorem
Bir üçgeni düşünün. açısının açıortayının ile arasındaki noktasında kenarını kesmesine izin verin. Açıortay teoremi, doğru parçasının uzunluğunun parçasının uzunluğuna oranının kenarının uzunluğunun kenarının uzunluğuna oranına eşit olduğunu belirtir:
ve tersine, üçgeninin kenarındaki noktası 'yi ve kenarları ile aynı oranda bölerse, daha sonra , açısının açıortayıdır.
Genelleştirilmiş açıortay teoremi, eğer , doğrusu üzerinde yer alıyorsa, o zaman
, 'nin açıortayıysa bu ifade, önceki sürüme indirgenir. , bölümünün dışında olduğunda, hesaplamada yönlendirilmiş çizgi bölümleri ve yönlendirilmiş açılar kullanılmalıdır.
Açıortay teoremi, açıortayları ve yan uzunlukları bilindiğinde yaygın olarak kullanılır. Bir hesaplamada veya bir ispatta kullanılabilir.
Teoremin doğrudan bir sonucu, bir ikizkenar üçgenin tepe açısının açıortayının aynı zamanda karşı kenarı ikiye böldüğüdür.
İspatlar
İspat 1
Yukarıdaki diyagramda, ve üçgenlerinde sinüs teoremi kullanıldığında:
-
(1)
-
(2)
ve açıları doğrusal bir çift oluşturur, yani bitişik bütünler açılar'dır. Bütünler açılar eşit sinüslere sahip olduğundan,
ve açıları eşittir. Bu nedenle, denklemlerin sağ tarafları (1) ve (2) eşittir, bu nedenle sol tarafları da eşit olmalıdır.
bu da açıortay teoremi'dir.
ve açıları eşit değilse, denklemler (1) ve (2) şu şekilde yeniden yazılabilir:
ve açıları hala bütünlerdir, bu nedenle bu denklemlerin sağ tarafları hala eşittir, dolayısıyla şunu elde ederiz:
bu ifade, teoremi "genelleştirilmiş" versiyona göre yeniden düzenler.
İspat 2

, doğrusu üzerinde bir nokta olsun, veya 'ye eşit olmasın ve , üçgeninin bir yüksekliği olmasın (yani doğrusuna dik olmasın).
, üçgeninin noktasından çizilen yüksekliğinin tabanı olsun ve , üçgeninin noktasından çizilen yüksekliğinin tabanı olsun. Daha sonra, kesinlikle ile arasındaysa, veya 'den biri ve yalnızca biri, üçgeninin içinde yer alır ve 'in genelliği kaybetmeden yaptığı varsayılabilir. Bu durum yandaki şekilde tasvir edilmiştir. , segmentinin dışında yer alıyorsa, o zaman ne ne de üçgenin içinde yer alır.
ve dik açılar iken, , segmentinde yer alıyorsa (yani, ve arasında) ve açıları eş açılardır ve dikkate alınan diğer durumlarda aynıdır, bu nedenle üçgenler ve benzerdir (AAA), yani
bir yüksekliğin tabanıysa, o zaman,
ve genelleştirilmiş biçime ulaşılır.
İspat 3

Hızlı bir kanıt, 'daki açıortay ile oluşturulan ve üçgenlerinin alanlarının oranlarına bakılarak elde edilebilir. Bu alanları farklı formüller kullanarak iki kez hesaplamak, yani taban ve yükseklik olmak üzere şeklinde ve , kenarlar ve bu kenarlar arasındaki açı olmak üzere şeklinde hesaplamak mümkün olup istenen sonucu verecektir.
, tabanı olan üçgenlerin yüksekliği ve 'daki açının yarısı olsun. Sonra,
ve
buradan da
bulunur.
Dış açıortaylar
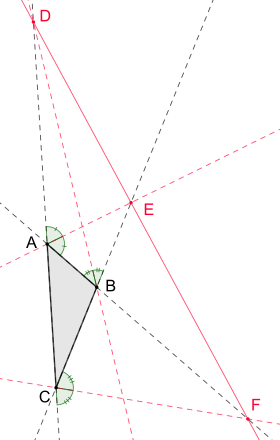
, , noktaları eşdoğrusaldır ve oranlar için aşağıdaki denklemler geçerlidir:
, ,
Eşkenar olmayan bir üçgendeki dış açıortaylar için, üçgen kenarlarının uzunluklarının oranları arasında benzer denklemler vardır. Daha doğrusu, 'daki dış açıortay 'de uzatılmış kenar ile kesişiyorsa, 'deki dış açıortay 'de uzatılmış kenar ile kesişir ve 'deki dış açı açıortay uzatılmış kenar ile 'de kesişir, ardından aşağıdaki denklemler geçerli olur:[1], ,
Dış açıortayları ile uzatılmış üçgen kenarları , ve arasındaki üç kesişme noktası eşdoğrusaldır, yani bir ortak çizgi üzerindedir.[2]
Tarihçe
Açıortay teoremi, Öklid'in Elemanları Kitap VI'nın Önerme 3'ü olarak görünür. Heath (1956, s. 197 (cilt 2))'e göre, dış açıortay için karşılık gelen ifade Robert Simson tarafından verildi ve Pappus bu sonucu kanıt olmadan doğru varsaydı. Heath, Augustus De Morgan'ın iki ifadenin aşağıdaki gibi birleştirilmesini önerdiğini söyler:[3]
| “ | Bir üçgenin bir açısı, karşı kenarı veya zıt kenarı kesen düz bir çizgi ile içten veya dıştan ikiye bölünürse, o tarafın dilimleri üçgenin diğer kenarları ile aynı orana sahip olacaktır ve eğer bir üçgenin bir kenarı, parçalarının üçgenin diğer kenarlarıyla aynı orana sahip olması için içten veya dıştan bölünüyorsa, kesit noktasından ilk bahsedilen kenarın karşısındaki açısal noktaya çizilen düz çizgi bu açısal noktada iç veya dış açıyı ikiye böler. | „ |
Notlar
- ^ Alfred S. Posamentier: Advanced Euclidian Geometry: Excursions for Students and Teachers. Springer, 2002, 9781930190856, pp. 3-4
- ^ Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, 978-0-486-46237-0, p. 149 (original publication 1929 with Houghton Mifflin Company (Boston) as Modern Geometry).
- ^ Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (2. ed. [Facsimile. Original publication: Cambridge University Press, 1925] bas.). New York: Dover Publications.
- (3 cilt): 0-486-60088-2 (cilt 1), 0-486-60089-0 (cilt 2), 0-486-60090-4 (cilt 3). Heath'in yetkili çevirisi ile birlikte kapsamlı tarihsel araştırma ve metin boyunca ayrıntılı yorumlar içerir.
Konuyla ilgili yayınlar
- G.W.I.S Amarasinghe (2012), "On the Standard Lengths of Angle Bisectors and the Angle Bisector Theorem", Global Journal of Advanced Research on Classical and Modern Geometries, 1 (1), ss. 15-27, 13 Ocak 2015 tarihinde kaynağından arşivlendi
Dış bağlantılar
- "A Property of Angle Bisectors". Cut-the-Knot. 24 Kasım 2005 tarihinde kaynağından arşivlendi.
- "Intro to angle bisector theorem". Khan Academy. 14 Kasım 2016 tarihinde kaynağından arşivlendi.






















































































