Matematik'sel olarak iki tam kare farkı bir sayının karesinden başka bir sayının karesinin çıkarılması sonucu elde edilen sayıya denir. Her bir iki tam kare sayı farkı, aşağıdaki temel cebir özdeşliğine göre çarpanlarına ayrılabilir.
Sayı, sayma, ölçme ve etiketleme için kullanılan bir matematiksel nesnedir. En temel örnek, doğal sayılardır. Sayılar, sayı adı (numeral) ile dilde temsil edilebilir. Daha evrensel olarak, tekil sayılar rakam adı verilen sembollerle temsil edilebilir; örneğin, "5" beş sayısını temsil eden bir rakamdır. Yalnızca nispeten az sayıda sembolün ezberlenebilmesi nedeniyle, temel rakamlar genellikle bir rakam sisteminde organize edilir, bu da herhangi bir sayıyı temsil etmenin organize bir yoludur. En yaygın rakam sistemi Hint-Arap rakam sistemidir, bu sistem on temel sayısal sembol, yani rakam kullanılarak herhangi bir negatif olmayan tam sayının temsil edilmesine olanak tanır. Sayılar sayma ve ölçme dışında, etiketlerde, sıralamada ve kodlarda kullanılmak için de sıklıkla kullanılır. Yaygın kullanımda, bir rakam ile temsil ettiği sayı net bir şekilde ayrılmaz.
Tam sayılar, sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar ve bunların negatif değerlerinden oluşan negatif sayılardan oluşan sayı kümesidir.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi 
Rasyonel sayılar, iki tam sayı arasındaki oranı temsil eden, bir pay p ve sıfırdan farklı bir payda q olmak üzere, bir bölme işlemi veya kesir formunda ifade edilebilen sayıları tanımlar. Örneğin, 
Matematikte, sıfır olmayan iki veya daha fazla pozitif tam sayının en büyük ortak böleni, tam sayıların hepsini de bölen en büyük pozitif tam sayıdır. Örneğin; 8 ve 12’nin ebob’u 4’tür.
Matematikte negatif olmayan bir gerçel 
1954 FIFA Dünya Kupası, Dünya Kupalarının beşincisi olan bu turnuva, İsviçre'de, 16 Haziran - 4 Temmuz 1954 tarihlerinde düzenlenmiştir. İsviçre, Temmuz 1946'da FIFA tarafından ev sahibi ülke olarak seçilmiştir. FIFA'nın 50. yılını kutladığı bir zamanda düzenlenen bu kupayı, son olimpiyat şampiyonu olan ve 28 maçtır da yenilmeyen Macaristan'ı 3-2 ile mağlup eden Batı Almanya tarihinde ilk defa kazanmıştır. Gruplardaki ilk maçı Macaristan'a karşı 8-3 kaybeden Batı Almanya, finalde rövanşı alarak oynadığı ilk 4 maçta tam 25 gol atan Macaristan'ın kupayı 2. kez finalde kaybetmesine sebep olmuştur. Avusturya turnuvayı 3. tamamlarken, Uruguay da 4. olmuştur. Ayrıca, İsviçre'deki turnuvada takımlar ilk kez numaralı formalarla sahaya çıkmışlardır.
Çıkarma, temel aritmetik işlemlerden biridir. İki sayının farkının alınması işlemidir. Azalma anlamı vardır. İki nokta arasındaki uzaklığı belirtir. Sonucun negatif olması, sonucun orijinden negatif yönde bir uzaklığa karşılık geldiğini gösterir.
Dizi, bir sıralı listedir. Bir küme gibi, ögelerden oluşur. Sıralı ögelerin sayısına dizinin uzunluğu denir. Kümenin aksine sıralı ve aynı ögeler dizide farklı konumlarda birkaç kez bulunabilir. Tam olarak bir dizi, tanım kümesi sayılabilen toplam sıralı kümelerden oluşan bir fonksiyon olarak tanımlanabilir. Örneğin doğal sayılar gibi. Diziler bu örnekte olduğu gibi sonlu olabilir. Ya da tüm çift pozitif tam sayılar gibi sonsuz olabilir.
Üs, bazen kuvvet, b taban, n üs veya kuvvet olmak üzere, bn olarak gösterilen ve "b üssü n", "b üzeri n" veya "b'nin n'inci kuvveti" olarak telaffuz edilen matematiksel işlem. Eğer n pozitif bir tam sayıysa, tabanın tekrarlanan çarpımına karşılık gelir:
Matematik, bilimde olduğu kadar günlük hayatımızda karşılaştığımız sorunların çözümünde kullandığımız önemli bir araçtır. Bundan dolayı matematikle ilgili davranışlar ilköğretimden yükseköğretim programına kadar her alanda yer alır. İlköğretimde ortaöğretime hazırlık olarak, ortaöğretimde yükseköğretime hazırlık olarak matematik öğretimi yapılır. Matematik öğretiminin temel amacı; kişiye günlük hayatın gerektirdiği matematik bilgi ve becerileri kazandırmak, problem çözmeyi öğretmektir. Matematik insan tarafından yaratılan zihinsel bir sistemdir. Bu matematiği soyut hale getirir. Görece, zor öğrenilmesinin sebebi budur. Öğretim sırasında somut araçlar kullanılarak kolaylaştırılabilir.
Cebirsel sayılar, rasyonel katsayıları olan tek değişkenli sıfırdan farklı bir polinomun kökü olarak ifade edilebilen sayılardır. Mesela, altın oran, 
Cebirde bir sayının karesi o sayının kendisiyle çarpılması sonucu elde edilen sayıdır. Karesi alınan x sayısı x² biçiminde yazılır.
Tam kare karekökü bir doğal sayı olan tam sayılara denir. Diğer bir deyişle, kendiyle çarpılan doğal sayıların sonucu tam karedir. 0, 1, 4, 9, 16, 25, 36, 49... ilk tam karelere örnektir.
Pearson ki-kare testi nicel veya nitel değişkenler arasında bağımlılık olup olmadığının, örnek sonuçlarının belirli bir teorik olasılık dağılımına uygun olup olmadığının, iki veya daha fazla örneğin aynı anakütleden gelip gelmediğinin, ikiden fazla anakütle oranının birbirine eşit olup olmadığının ve çeşitli anakütle oranlarının belirli değere eşit olup olmadığının araştırılmasında kullanılır. İstatistik biliminin çıkarımsal istatistik bölümünde ele alınan iki-değişirli parametrik olmayan test analizlerinden olan ve ki-kare dağılımı'nı esas olarak kullanan ki-kare testlerinden en çok kullanılanıdır. İngiliz istatistikçi olan Karl Pearson tarafından 1900'da ortaya çıkartılmıştır.
Matematikte özdeşlik, bilinmeyenin her değeri için doğru olan açık eşitliklerdir.
Çarpanlara ayırma, bir polinomun, tam sayının ya da matrisin kendisini oluşturan bileşenlerin çarpımı şeklinde yazılmasıdır. Örneğin 15 sayısı 3 ve 5 asal sayılarının çarpımı şeklinde yazılabilir: 3 × 5 ya da x2 − 4 polinomu (x − 2)(x + 2) şeklinde yazılabilir.
Cyreneli Theodorus, MÖ 5. yüzyılda yaşamış eski bir Libyalı Yunan matematikçi. Günümüze ulaşan ve ilk elden anlatılanlar, Platon'un diyaloglarından üçünde; Theaetetus, Sofist ve Devlet Adamı (Statesman) yer alır. Önceki diyalogda, şimdi Theodorus Sarmalı olarak bilinen matematiksel bir teoremi öne sürmektedir.
Bu, Wikipedia'da yer alan sayı teorisi konularıyla ilgili sayfaların bir listesidir.
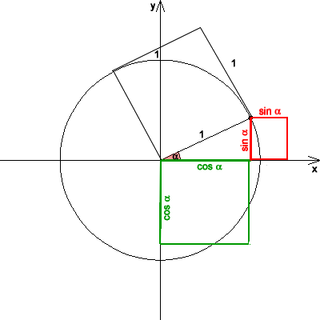
Pisagor trigonometrik özdeşliği, daha basit ifadeyle Pisagor özdeşliği olarak da adlandırılır, Pisagor teoremini trigonometrik fonksiyonlar cinsinden ifade eden bir özdeşliktir. Açıların toplam formülleri ile birlikte, sinüs ve kosinüs fonksiyonları arasındaki temel bağıntılardan biridir. Özdeşlik şu şekildedir:
