Graf teorisi, çizge teorisi veya çizit teorisi, grafları inceleyen matematik dalıdır. Graf, düğümler ve bu düğümleri birbirine bağlayan kenarlardan oluşan bir tür ağ yapısıdır. Bir graf, çizge veya çizit, düğümlerden (köşeler) ve bu düğümleri birbirine bağlayan kenarlardan oluşur.
Tam sayılar, sayılar kümesinde yer alan sıfır (0), pozitif yönde yer alan doğal sayılar ve bunların negatif değerlerinden oluşan negatif sayılardan oluşan sayı kümesidir.
Doğal sayılar, 
şeklinde sıralanan tam sayılardır ve kimi tanımlamalara göre 0 sayısı da bu kümeye dâhil edilebilir. Aralarında standart ISO 80000-2'nin de bulunduğu bazı tanımlar doğal sayıları 0 ile başlatır ve bu durum negatif olmayan tam sayılar için 0, 1, 2, 3, ... şeklinde bir karşılık bulurken, bazı tanımlamalar 1 ile başlamakta ve bu da pozitif tam sayılar için 1, 2, 3, ... şeklinde bir eşlenik oluşturur. Doğal sayıları sıfır olmadan ele alan metinlerde, sıfırın da dahil edildiği doğal sayılar bazen tam sayılar olarak adlandırılırken diğer bazı metinlerde bu terim, negatif tam sayılar da dahil olmak üzere tam sayılar için kullanılmaktadır. Özellikle ilkokul seviyesindeki eğitimde, doğal sayılar, negatif tam sayıları ve sıfırı dışlamak ve saymanın ayrık yapısını, gerçek sayıların bir karakteristiği olan ölçümün sürekliliğiyle karşıtlık oluşturmak amacıyla sayma sayıları olarak adlandırılabilir.
Matematikte reel sayılar kümesi, Fransızca réel “gerçek” den gelmektedir. Oranlı sayılar kümesinin evrim sürecinden elde edilen bir varsayım kombinasyonudur. Reel sayılar kümesi 
sembolüyle gösterilir.
Tıkızlık, topolojik uzayların sahip olabileceği başlıca özelliklerden biridir. Bir X uzayı ve birleşimleri X uzayını kaplayan herhangi bir açık kümeler topluluğu verildiğinde, bu topluluğun içinden sonlu sayıda açık küme hala X uzayını kaplayabiliyorsa, X uzayına tıkız (kompakt) denir. Gerçel sayılar kümesi (ℜ), üzerindeki standart topolojiye göre tıkız değildir, ancak ℜ’nin her kapalı ve sınırlı alt kümesi altuzay topolojisine göre tıkızdır. Matematiğin diğer pek çok alanında olduğu gibi, sonsuz bir nesnenin sonlu bir nesneye indirgenebilmesi çok önemli avantajlar sağladığı için topoloji alanında ve topolojik yöntemler kullanan diğer alanlarda vazgeçilmez bir kavramdır.
Fonksiyon, matematikte değişken sayıları girdi olarak kabul edip bunlardan bir çıktı sayısı oluşmasını sağlayan kurallardır. Fonksiyon, 17. yüzyılda matematiğin kavramlarından biri olmuştur. Fizik, mühendislik, mimarlık ve birçok alanda kullanılmaktadır. Galile, Kepler ve Newton hareketlerin araştırılmasında, zaman ve mesafe arasındaki durumu incelemek için fonksiyonlardan faydalanmıştır. Dört işlemden sonra gelen bir işlem türüdür.
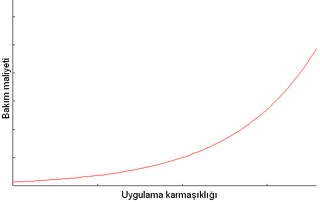
Nesne yönelimli programlama veya kısaca NYP, Her işlevin nesneler olarak soyutlandığı bir programlama yaklaşımıdır. NYP destekleyen programlama dilleri yüksek seviye diller olarak adlandırılır.
Halka, matematikte cebirin temel yapılarından biridir ve soyut cebirde tam sayıların soyutlamasıdır. Bu yapıyı işleyen dala halka kuramı denir. Halkalar diğer bir temel yapı olan grupların üzerine inşa edilir. Her halka, aynı zamanda değişmeli bir gruptur, ama bir halkadan daha fazla özelliği sağlaması istenir. Örneğin halkada grup işlemine ek olarak ikinci bir işlem daha vardır. Halkalara örnek olarak tam sayılar, modülo n sayılar, polinomlar ya da karmaşık sayılar verilebilir.
Matematikte birim öge, birim eleman, etkisiz eleman veya nötr eleman, bir kümenin özel bir ögesidir. Bir kümede herhangi bir ögeyle işleme girdiğinde yine aynı ögeyi verir. Genel olarak e ile gösterilir.
- Her a
A için öyle bir e A vardır ki ea=ae=a olur.
Küresel yıldız kümesi, galaksi merkezi etrafında uydu gibi dolanan, yıldızların küresel bir bileşimidir. Küresel yıldız kümeleri yerçekimi ile bir arada durabilirler. Yerçekimi sayesinde küresel bir şekle ve göreceli olarak merkeze doğru artan bir madde yoğunluğuna sahiplerdir. Yıldız kümesinin bir alt kategorisi olan küresel yıldız kümesi, Latince bir sözcük olan ve küçük küre anlamına gelen globulus kelimesinden türetilmiştir.
Yıldız kümeleri veya yıldız bulutları, öz kütleçekimiyle bir arada tutulan büyük yıldız gruplarıdır. İki ana yıldız kümesi türü belirlenmiştir: Küresel kümeler, kütleçekimsel olarak bağlı on bin ila milyonlarca yaşlı yıldızın oluşturduğu sıkı gruplardır, açık kümeler ise genellikle birkaç yüzden az üye içeren, daha gevşek kümelenmiş ve çoğunlukla çok genç yıldızların oluşturduğu gruplardır. Açık kümeler, gökada içinde hareket ederken dev moleküler bulutların çekim etkisiyle zamanla dağılır, fakat küme üyeleri artık çekimsel olarak bağlı olmasalar da uzayda genel olarak aynı yönde hareket etmeye devam ederler; bunlara yıldız topluluğu, bazen de hareketli grup denir.
Dizi, bir sıralı listedir. Bir küme gibi, ögelerden oluşur. Sıralı ögelerin sayısına dizinin uzunluğu denir. Kümenin aksine sıralı ve aynı ögeler dizide farklı konumlarda birkaç kez bulunabilir. Tam olarak bir dizi, tanım kümesi sayılabilen toplam sıralı kümelerden oluşan bir fonksiyon olarak tanımlanabilir. Örneğin doğal sayılar gibi. Diziler bu örnekte olduğu gibi sonlu olabilir. Ya da tüm çift pozitif tam sayılar gibi sonsuz olabilir.
Küme kuramında, birleşme, bir kümenin tüm ögelerinin topluluğudur ve ∪ ile sembolize edilir.
Vektör uzayı veya Yöney uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesnelerin (vektörlerin) uzayına verilen isimdir. Daha resmî bir tanımla, bir vektör uzayı, iki elemanı arasında vektör toplamasının ve skaler denilen sayılarla çarpımın tanımlı olduğu ve bunların bazı aksiyomları sağladığı kümedir. Skalerler, rasyonal veya reel sayılar kümesinden gelebilir, ama herhangi bir cisim üzerinden bir vektör uzayı oluşturmak mümkündür. Vektör uzayları, skalerlerin geldiği cisime göre reel vektör uzayı, kompleks vektör uzayı veya genel bir cisim üzerinden K vektör uzayı şeklinde adlandırılır.
Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.
Matematikte fonksiyon uzayı bir X kümesinden bir Y kümesine tanımlı fonksiyonların oluşturduğu kümeye verilen bir addır. Fonksiyonlar kümesi yerine fonksiyon uzayı denilmesinin nedeni matematiğin kendi içindeki uygulamalarında bu kümenin genellikle topolojik uzay veya vektör uzayı olarak ortaya çıkmasıdır.
Açık yıldız kümeleri, birkaç bin yıldızdan oluşan bir yıldız grubudur. Açık yıldız kümesini oluşturan yıldızlar aynı dev moleküler buluttan oluşmuşlardır ve yaklaşık olarak aynı yaştadırlar. Açık yıldız kümesi galaktik küme olarak da bilinir. Samanyolu Galaksisi'nde 1100'den fazla açık yıldız kümesi keşfedilmiştir ve daha fazla olduğu düşünülmektedir. Açık yıldız kümeleri karşılıklı yerçekimi etkisiyle birbirlerine gevşek bir biçimde bağlıdırlar. Açık yıldız kümeleri diğer kümelerle ve gaz bulutlarıyla yakın temaslarda bulunarak bozulmuş hale gelirler. Bu bozulmalar hem galaksinin ana bölümüne doğru yer değiştirmelere hem de küme elemanlarının yakın temasların içine doğru kaybıyla sonuçlanır.
Eşyapı ya da izomorfizma (ya da izomorfi), aynı kategoride(grupta) olan benzer iki matematiksel obje arasında bir gönderim olup matematiksel vücut tersi yapıda da muhafaza edilir. Aralarında bu şekilde eşyapı bulunan objelere eşyapısal ya da izomorf(ik) objeler denir. Örneğin iki küme arasında eşyapı, birebir, örten bir gönderimdir. Kümelerin üzerinde elemanlara sahip olma haricinde bir oluşum olmadığından, eşyapı gönderiminin koruyacağı başka bir yapı yoktur. Soyut cebirde iki grup arasında bir eşyapı, birebir, örten bir gönderimdir; dahası, iki gruptaki işleme saygı gösterir, bu iki işlemin birbirleriyle etkileşim halinde olmasını sağlar.
Birebir örten fonksiyon, matematikte hem birebir hem örten fonksiyon özelliklerini aynı anda gösteren fonksiyonlardır. İki küme arasındaki fonksiyonda 1.kümeden her bir eleman ikinci kümedeki elemanla eşleşir ve her iki kümeden açıkta eleman kalmaz. Örten fonksiyon görüntü kümesinde boşta eleman kalmayacak şekilde eşleşmenin gerçekleştiği, birebir fonksiyon ise her bir elemanın diğer kümenin bir elmanıyla eşleştiği fonksiyondur. Birebir örten fonksiyonlar ise bu iki fonksiyonun özelliklerine aynı anda sahip olan fonksiyonlardır.
Serbest hatırlama, belleğin psikolojik açıdan çalışılmasında kullanılan temel bir paradigmadır. Bu modelde, katılımcılar her bir denemedeki ögelerin bir listesini inceler ve ardından onlardan ögeleri herhangi bir sırada hatırlamaları istenir. Ögeler kişilere genellikle birer birer, kısa süreli olarak sunulur ve bu ögeler adlandırılabilen herhangi bir materyal grubundan seçilebilir. Hatırlama süresi tipik olarak birkaç dakika sürer ve sözlü veya yazılı hatırlamayı içerir. Standart model, listedeki son ögeden hemen sonra başlayan hatırlama süresini içerir; bu, gecikmiş serbest hatırlama (DFR) 'dan ayırt etmek için anında serbest hatırlama (IFR) olarak adlandırılabilir. Gecikmeli serbest hatırlama işleminde, listedeki son öge ile hatırlama sürecinin başlangıcı arasında dikkat dağıtıcı kısa bir süre yer alır. Bu bağlamda hem anında serbest hatırlama hem de gecikmeli serbest hatırlama, hatırlama testleri sırasında ortaya çıkan ilklik etkisi ve sonluk etkisi gibi belirli etkileri test etmek için kullanılmıştır.