Grup teorisi veya Grup kuramı, simetrileri inceleyen matematik dalıdır. Simetri kuramı olarak da adlandırılabilir. Bir nesnenin simetrileri ile kast edilen, nesneye uygulandığında nesneye hiçbir etki olmamış gibi sonuç veren dönüşümlerdir. Her nesnenin en az bir simetrisi vardır: hiçbir şey yapmadan olduğu gibi bırakma dönüşümü. Bahsettiğimiz dönüşümlerin tersleri de vardır ve aradığımız özellikleri sağlarlar. Son olarak da dönüşümlerin art arda yapılması, birleşimli bir işlemdir. Bu üç koşula sırasıyla birim elemana sahip olma, elemenların tersi olma ve grup işleminin birleşmeli olması denir. Bu kavramların matematikte soyutlanması, üzerinde tersinebilir ve bileşme özelliğine sahip ikili bir işlemin tanımlı olduğu kümeler ile yapılır. Daha detaylı açıklamak gerekirse, grup nesnesi bir küme G ve onun üzerinde tanımlı bir  işleminden oluşur. Bu operasyonun aşağıdaki şartları sağlaması gereklidir:
işleminden oluşur. Bu operasyonun aşağıdaki şartları sağlaması gereklidir:

Leonhard Euler, çizge teorisi çalışmasını kuran bir İsviçreli matematikçi, fizikçi, astronom, coğrafyacı, mantıkçı ve mühendisti. Topoloji ve analitik sayı teorisi, karmaşık analiz ve sonsuz küçük hesap gibi matematiğin diğer birçok dalında öncü ve etkili keşifler yaptı. Bir matematiksel fonksiyon kavramı da dahil olmak üzere, modern matematiksel terminolojinin ve gösterim'in çoğunu tanıttı. Ayrıca mekanik, akışkan dinamiği, optik, astronomi ve müzik teorisi alanındaki çalışmalarıyla da tanınır.
Ağ modeli yöneylem araştırmasında belirlenmiş bir sıra problemin düğümler ve dal veya bağlantilardan oluşan bir şebeke halinde tanımlanıp modellemesi türü olup ve tanımlanan sebeke problemlerinin çözümlenmesi için ortaya çıkartılan özel şebeke problemi algoritmalardan oluşur. Bu türlü çalışmalarda önce problemin ögeleri ve amacı tarif edilir. Sonra problemin şekil olarak veya matris olarak dallar ile birbirlerine bağlı düğümler halinde yapılandırılıp tanımlanması gerekir. Örneğin problem bir şehre kurulacak su borusu şebekesinin, bütün şehre en ucuz maliyet ile nasıl kurulacağıdir. Bu problem bir mümkün olan bütün bağlantı parçalarını, maliyetleri ve kapasiteleri gösteren şebeke halinde ifade edilir. Bu problem ve yapılanan model bir minimum maliyet kapasiteli sebeke problemi olduğu için bu çeşit model problemi çözmek için geliştirilmiş olan özel algoritmalardan birini kullanarak çözülebilir.

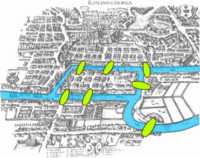
Königsberg'in yedi köprüsü; graf teorisinin temelini oluşturan ve XVIII. yüzyılda Königsberg köprülerinden ilhamlanılarak ortaya atılan ünlü bir matematik problemidir.

Küme, matematikte farklı nesnelerin topluluğu veya yığını olarak tanımlanmaktadır. Bu tanımdaki "nesne" soyut ya da somut bir şeydir. Fakat her ne olursa olsun iyi tanımlanmış olan bir şeyi, bir eşyayı ifade etmektedir. Örneğin, "Tüm canlılar topluluğu", "Dilimiz alfabesindeki harflerin topluluğu", "Masamın üzerindeki tüm kâğıtlar" tümcelerindeki nesnelerin anlaşılabilir, belirgin oldukları, kısaca iyi tanımlı oldukları açıkça ifade edilmektedir. Dolayısıyla bu tümcelerin her biri bir kümeyi tarif etmektedir. O halde, matematikte "İyi tanımlı nesnelerin topluluğuna küme denir." biçiminde bir tanımlama yapılmaktadır.
Bağıntıda yansıma, simetri ve geçişme özelliği varsa bu bağıntı denklik bağıntısıdır.
Hamilton Yolu, yönlü veya yönsüz bir grafta Hamilton yolu veya Hamilton devresinin olup olmadığının kararının verilmesinin problemidir.
3SAT ve KLIK problemleri, Turing makinasından polinom zamanda kararlaştırılabilen NP problemleri arasında yer alır. Bu problemlerin birbirinin cinsine çevrilmesine indirgeme denilir.
Köşe Örtme, bir çizge (graf) içerisindeki tüm kenarların en az sayıda seçilebilecek düğüm ile kapsanabilir olup olmadığının bulunması problemidir. Bu problemin NP sınıfı içerisinde olduğu bilinmektedir. Amaç, bu problemin NP-Tam sınıfında olup olmadığının ispatıdır.
Arama algoritmaları, bilgisayar biliminde seçili özelliklere göre istenilen bilgileri bulan algoritmalardır. Listeler, metinler ve şekiller üzerinde çalışırlar.
Sıra teorisi, ikili bağıntıları kullanma sırasının sezgisel kavramını inceleyen bir matematik dalıdır. "Bu, şundan daha küçüktür" veya "bu, şundan daha öncedir" gibi durumları inceler.
Hamilton yolu problemi, Hamilton yolunun çözümü ile ilgili problemdir.
Eşyapı ya da izomorfizma (ya da izomorfi), aynı kategoride(grupta) olan benzer iki matematiksel obje arasında bir gönderim olup matematiksel vücut tersi yapıda da muhafaza edilir. Aralarında bu şekilde eşyapı bulunan objelere eşyapısal ya da izomorf(ik) objeler denir. Örneğin iki küme arasında eşyapı, birebir, örten bir gönderimdir. Kümelerin üzerinde elemanlara sahip olma haricinde bir oluşum olmadığından, eşyapı gönderiminin koruyacağı başka bir yapı yoktur. Soyut cebirde iki grup arasında bir eşyapı, birebir, örten bir gönderimdir; dahası, iki gruptaki işleme saygı gösterir, bu iki işlemin birbirleriyle etkileşim halinde olmasını sağlar.

Graf teorisinde, düğümleri her kenar iki kümede de birer bitiş ucuna sahip olacak şekilde iki ayrı kümeye ayrılabilen graflara iki parçalı graf adı verilir.

Bir Bayes ağı, Bayes modeli ya da olasılıksal yönlü dönüşsüz çizge modeli bir olasılıksal çizge modelidir ve birbirleriyle koşulsal bağımlılıklara sahip bir rassal değişkenler kümesini yönlü dönüşsüz çizge(YDÇ) şeklinde ifade eder. Bayes ağları; gündelik hayatta meydana gelen bir olayı anlatmak ve o olayın gerçekleşmesine sebebiyet verebileceği bilinen birkaç olası nedenden herhangi birinin katkıda bulunan faktör olma olasılığını tahmin etmek için kullanılan ideal bir modelleme türüdür. Örneğin, bir Bayes ağı kullanılarak hastalıklar ve semptomları arasındaki olasılıksal koşul ilişkileri modellenebilir. Bu model kullanılarak, bir kişide görülen semptomlar verildiğinde bu kişinin bazı hastalıklara sahip olma olasılıkları hesaplanabilir. Buna benzer olarak neden-sonuç ilişkisi olan birçok olayın olasılığı bu modelleme ile görselleştirilebilir.

Düğüm matematikte ve özellikle çizge teorisinde, bir çizgeyi oluşturan temel elemandır. Bir çizge temel olarak düğüm ve kenarlardan oluşur. Çizge görselleştirilirken genellikle düğümler çember, kenarlar da çizgi veya ok şeklinde gösterilir.

Matematikte graf ya da çizge, nesne çiftlerinin bir anlamda "ilişkili" olduğu bir dizi nesne kümesini belirleyen bir yapıdır. Nesneler, köşeler adı verilen matematiksel soyutlamalara karşılık gelir ve ilgili düğüm çiftlerinin her birine bir kenar, ayrıt adı verilir. Tipik olarak bir graf, kenarları için çizgiler veya eğriler ile birleştirilen, düğümler için bir nokta veya daire kümesi olarak diyagram şeklinde gösterilir. Graflar ayrık matematikte çalışmanın amaçlarından biridir.

Çizge teorisinde, yönlü çizge düğümler ve hepsi birer yöne sahip kenarlardan oluşan çizgedir.
Pólya'nın sayma teoremi, bir küme üzerindeki bir grup davranışının yörünge sayısını veren Burnside önsavını izleyen ve genelleştiren bir kombinatorik teoremidir. Teorem; ilk olarak 1927 yılında J. Howard Redfield tarafından yayımlanmış, 1937'de ise teoremin ortaya çıkardığı sonuçları birçok sayma problemine, özellikle kimyasal bileşiklerin sayımına uygulayarak büyük ölçüde yaygınlaştıran George Pólya tarafından yeniden keşfedilmiştir.