Altın oran, matematikte iki miktardan büyük olanın küçüğe oranı, miktarların toplamının miktarları büyük olanına oranı ile aynı ise altın orandır. Altın oran aynı zamanda antik çağdan bu yana sanat ve mimaride en iyi uyum ve oranları veren düzen bağıntısı olarak kabul edilmekteydi.

Sinüs teoremi, bir çembersel üçgende bir kenar ve bu kenar karşısındaki açının sinüsleri oranı sabittir. Sinüs, dik açılı üçgenlerde dik olmayan bir açının karşısında kalan dik kenar ile hipotenüsün birbirine oranıdır.
Alan veya yüz ölçümü, bir yüzeyin uzayda kapladığı iki boyutlu yer miktarını ölçen bir büyüklüktür. SI birim sisteminde temel alan birimi metrekaredir (m²). Diğer alan birimleri bundan türetilebilir:
- Ar = 100 metrekare (m²)
- Dekar = 1000 metrekareye (m²)
- Hektar = 10.000 metrekare (m²)
- Kilometrekare = 1.000.000 metrekare (m²)

Konik kesit, eliptik veya dairesel bir çift taraflı koninin, düzlemle kesitinden meydana gelen eğriler. Bunlar, çember, elips, parabol ve hiperboldür.

Koni, matematikte, bir düzlem içindeki dairenin her noktasını, düzlem dışındaki bir noktaya birleştiren doğru parçalarının meydana getirdiği geometrik şekil.

Parabol, bir düzlemde alınan sabit bir "d" doğrusu ile sabit bir "F" noktasından eşit uzaklıktaki noktaların geometrik yerleştirilmesidir. Cebirde ise y=ax2+bx+c şeklindeki ikinci derece fonksiyonları grafiği olarak bilinir.

Düzgün dairesel hareket, sabit bir kuvvetin etkisinde, bir çember üzerinde süratin değişmediği harekettir.
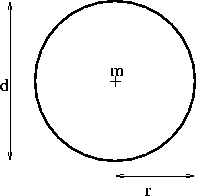
Çap, bir çemberin merkezinden geçen ve çemberi iki eşit parçaya bölen doğru çizgisine verilen addır ve yarıçap'ın 2 katı uzunluğundadır.  ile çarpılırsa o çemberin çevresi bulunur.
ile çarpılırsa o çemberin çevresi bulunur.

Matematikte sinüs, trigonometrik bir fonksiyon. Sin kısaltmasıyla ifade edilir.

Radyan, bir dairede yarıçap uzunluğundaki yay parçasını gören merkez açıya eşit açı ölçme birimidir. 1 radyan 180/π ya da yaklaşık 57,2958 derecedir (57°17′45″).

Daire ya da dönge, çemberin içinde kalan alana verilen isimdir. Burada alandan kasıt, bir çemberin çevrelediği noktaların kümesi olmasıdır. Bir dairenin açık daire ya da kapalı daire olmasını dairenin sınırlarını oluşturan çemberin daireye dahil olup olmadığı belirler; çember daireye dahilse kapalı daire, değilse açık dairedir.

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.
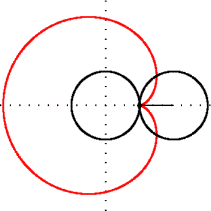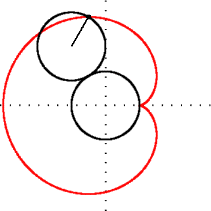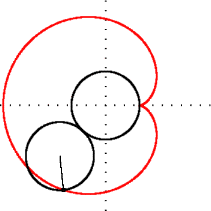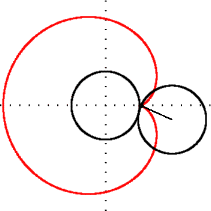
Matematikte kardiyoit veya yürek eğrisi, sabit bir çember üzerinde yuvarlanmakta olan aynı yarıçaplı ikinci bir çember üzerindeki herhangi bir noktanın izlediği eğridir. İsmi Yunanca kardia (kalp) ve eidos (şekil) kelimelerinin birleşiminden oluşur. Kalp (♥) şeklini anımsattığı için bu ismi almıştır. Kardiyoit ismini ilk kullanan, 18. yüzyıl İtalyan matematikçisi Johann Castillon olmuştur.
Jeostatik yörünge ya da Yer sabit yörünge, Dünya’nın çevresinde Dünya ile aynı dönme süresine sahip ve yerden bakılınca uzayda konumu sabit olan yapay uydu için hesaplanan yörünge. Yer sabit yörünge için yer yüzeyinden itibaren yükseklik sınırı 35.786 kilometredir. Bu yörüngede yer alan bir cisim, yerdeki sabit bir gözlemciye gökyüzündeki sabit bir nokta şeklinde görülecektir.
Açısal frekans periyodik harekette birim zaman içinde kaç radyan olduğunun ölçüsüdür.

Birim çember Matematikte, yarıçapı bir birim olan çembere birim çember denir. Çoğunlukla, özellikle trigonometride, Öklid düzlemine göre Kartezyen koordinat sisteminde, merkezi orijin üzerinde (0,0) olan ve yarıçapı bir birim olan çemberdir. n birim çember sıklıkla S1; olarak ifade edilir. Genellikle daha büyük boyutları ise birim küredir. (x, y) birim çember üzerinde bir nokta olduğunda, |x| ve |y|, dik olan ve hipotenüsü bir olan üçgenin diğer kenar uzunluklarıdır. Bu nedenle, Pisagor teoremine göre, x ve y bu denklemi karşılamaktadır.


Öklid geometrisinde, bir çift merkezli dörtgen, hem bir iç teğet çembere hem de çevrel çembere sahip olan bir dışbükey (konveks) dörtgendir. Bu çemberlerin çevreleri, yarıçapları ve merkezlerine sırasıyla iç çap (inradius) ve çevrel çap (circumradius), iç merkez (incenter) ve çevrel merkez (circumcenter) denir. Tanımdan, çift merkezli dörtgenlerin hem teğetler dörtgeninin hem de kirişler dörtgeninin tüm özelliklerine sahip olduğu anlaşılmaktadır. Bu dörtgenler için diğer isimler kiriş-teğet dörtgeni ve iç teğet ve dış teğet dörtgenidir. Ayrıca nadiren çift çemberli dörtgen ve çift işaretlenmiş dörtgen olarak adlandırılmıştır.
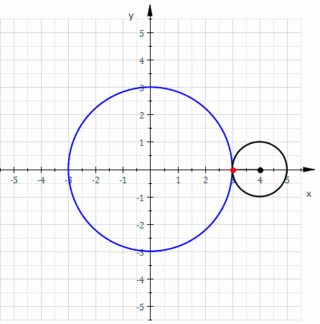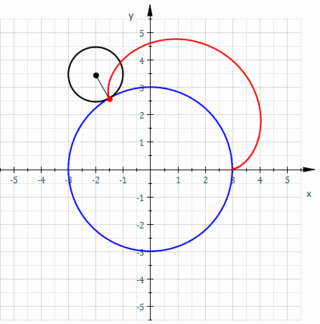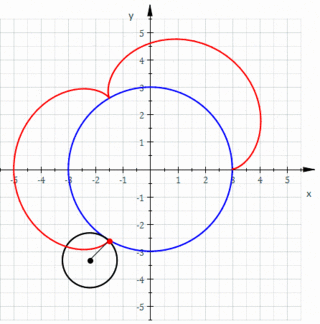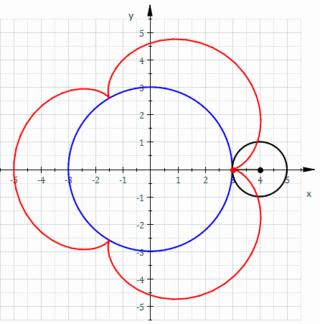
Geometride, bir episikloid, sabit bir çemberin etrafında kaymadan yuvarlanan bir çemberin çevresi üzerinde seçilen bir noktanın yolunu izleyerek üretilen bir düzlem eğrisidir -buna episikl (epicycle) denir. Bu, yuvarlanma eğrisinin özel bir türüdür.
Geometride, bir çokgenin yarı çevresi, çevre uzunluğunun yarısıdır. Çevreden doğrudan türetilebilmesine rağmen, yarı çevre üçgenler ve diğer şekiller için kullanılan formüllerde oldukça sık görülür ve ayrı/özel bir isim verilir. Yarı çevre, bir formülün parçası olarak ortaya çıktığında, genellikle s harfiyle gösterilir.





























