Çarpma algoritmaları
Çarpma algoritmaları, çarpma işlemi için gereken sonlu işlemler kümesidir. Çarpma işlemi, aritmetik işlemlerinde sık kullanılan ve bilimsel uygulamalarda önemli rolü olan, temeli aslında toplama ve kaydırma işlemlerine dayanan aritmetiksel bir işlemdir. Toplama işleminden daha karmaşıktır ve daha çok zaman alır aynı zamanda daha çok alan gerektirir.
Bilimsel programdaki komutların hemen hemen %9’u çarpma işlemi gerektirmektedir. Çarpma işlemi bir işlemcide 2 ile 8 saat çevrimi arası kadar bir zamanda yapılabilir. Bu yüzden, bir işlemcinin başarımını belirleyen en kritik ve önemli faktörlerden biri de çarpma algoritmalarının iyileştirilmesiyle birlikte bunların donanımda hızlı ve etkin uygulamasıdır.
Çarpma yöntemleri
Sıralı toplama/Kaydırma çarpma algoritması
Sıralı toplama/kaydırma algoritmasının temelinde çarpan sayısının en anlamsız basamağının bitinin değerine bakılır.
Çarpma algoritması 1. yol

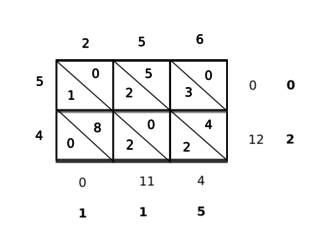
Çarpma algoritmalarından ilkinin yapılabilmesi için 64-bit çarpılan yazmacı, 64-bit AMB, 64-bit çarpım yazmacı, 32-bit çarpan yazmacı gerekmektedir. Bu algoritmanın çalışması için sağ taraftaki gibi bir donanıma ihtiyacı vardır. Algoritma genel olarak şu şekilde çalışmaktadır (n değeri 32 olarak alınmıştır): Her bir saat çevriminde çarpan bir bit sağa kaydırılır ve bu bitin değeri dikkate alınır. Son bit eğer '1' ise çarpılan değer çarpıma eklenir ve sonuç çarpım yazmacına yazılır. Bu işlemden sonra çarpılan yazmacı sola 1 bit kaydırılırken, çarpan yazmacını da sağa 1 bit kaydırılır. Çarpılan kaydırılırken sağına sıfırlar eklemeyi de unutmamak gerekir. Ancak ilk aşamada kontrol edilen çarpan yazmacının son biti '0' ise o zaman sadece çarpılan yazmacı sola 1 bit kaydırılırken, çarpan yazmacını da sağa 1 bit kaydırılır. Aşağıdaki kısa örnek algoritmanın nasıl işlediği hakkında bilgi vermektedir.
Yukarıdaki örnekte de görüldüğü gibi çarpan sayısının son biti 1'dir. Bu sebepten algoritma sol taraftaki yolu izler ve çarpılan sayı (0000 0010) çarpıma eklenir, böylece ikinci satırdaki çarpım sonucu bulunur, daha sonra çarpılan yazmacı 1 bit sola kaydırılır ve 2. satırdaki sonuç (0000 0100) elde edilmiş olur. Aynı şekilde algoritmayı takip edecek olursak çarpan yazmacı da sağa 1 bit kaydırılır ve ikinci satırdaki 0001 sonucu elde edilir. Yine aynı şekilde ikinci satırda da çarpan değerinin son biti 1 olduğu için aynı yöntem uygulanır; böylece üçüncü satırı elde etmiş oluruz. Üçüncü satırda çarpan bitinin 0 olduğu görülmektedir bu sebepten algoritmayı uygularken, algoritmanın sol kolu takip edilir ve çarpım yazmacına herhangi bir değer eklemeyeceğimizden bu sonucu değiştirmez ve aynen kalır; dolayısıyla çarpan yazmacı sürekli 0000 lardan oluşacağı için yani her defasında son biti 0 olacağı için sonuç aynı kalır.
Çarpma algoritması 2. yol

Bu algoritmalarda ikincisinin yapılabilmesi için ise 32-bit çarpılan yazmacı, 32-bit AMB, 64-bit sonuç yazmacı, 32-bit çarpan yazmacı gerekmektedir. Algoritmanın işleyişi aşağıdaki gibidir: İlk yolda olduğu gibi yine çarpan yazmacının son bitine bakılır. Son bit eğer '1' ise çarpılanla çarpımın sol yarısı toplanır ve sonuç çarpım yazmacının sol yarısına yazılır. Bu işlemden sonra çarpım yazmacı sağa 1 bit kaydırılırken çarpan yazmacı da sağa 1 bit kaydırılır. Son bit '0' ise herhangi bir işlem yapılmaksızın yine çarpım yazmacı sağa 1 bit kaydırılırken çarpan yazmacı da sağa 1 bit kaydırılır. Sonuç olarak çarpım yazmacı çarpanın boyutu kadar bir alanı israf eder. Çarpım yazmacının israf edilen alanı azaldıkça çarpandaki geri kalan bitlerin sayısı da azalır. Daha sonrasında ise n değeri kontrol edilir ve eğer 32'den küçükse döngü devam eder, değilse döngüden çıkar. Kısacası algoritmada n değeri 32 alındığı için bu algoritma 32 kez tekrarlanacaktır.
Çarpma algoritması 3. yol
Çarpma algoritmalarının 3. yolunda 32-bit çarpılan yazmacı, 32 -bit AMB, 64-bit çarpım yazmacı, (0-bit çarpan yazmacı) gerekmektedir. Algoritmanın işleyişi ise şu şekilde çalışmaktadır: Her bir saat çevriminde çarpım bir bit sağa kaydırılır ve bu bitin değeri test edilir. Çarpım yazmacının son bitinin değeri '0' ise sadece kaydırma işlemi gerçekleşirken, bitin değeri '1' ise çarpılan sayının değeri çarpımın sol yarısına eklenir ve sonuç çarpım yazmacının sol yarısına yazıldıktan sonra değeri bir bit sağa kaydırılır. Çarpan sayının tüm bitleri test edildikten sonra 2n uzunluğunda sonuç elde edilir. Burada gecikme değeri en fazla n çevrim zamanı kadar olur.[1]
Resim galerisi
- Çarpma algoritması 1. yol
- Çarpma algoritması 1. yol
- Çarpma algoritması 2. yol
- Çarpma algoritması 2. yol
- Çarpma algoritması 3. yol
- Çarpma algoritması 3. yol
Kaynakça
- ^ "Strassen algorithm for polynomial multiplication". everything2. 10 Ağustos 2016 tarihinde kaynağından arşivlendi. Erişim tarihi: 10 Eylül 2013.