İçeriğe atla

Çıkış düğümü boylamı

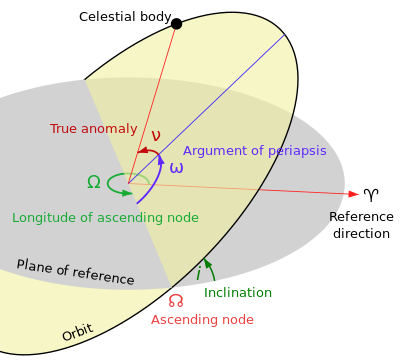
Yörünge ögeleri diyagramının bir parçası olarak çıkış düğümün boylamı (parlak yeşil).

Çıkış düğümü boylamı (☊ veya Ω), bir nesnenin uzaydaki yörüngesini belirtmek için kullanılan yörünge ögelerinden biridir. Belirtilen bir referans düzleminde ölçüldüğü gibi, boylamın orijini olarak adlandırılan belirli bir referans yönünden çıkış düğümün yönüne olan açıdır.[1] Çıkış düğümü, bitişik görüntüde görüldüğü gibi, nesnenin yörüngesinin referans düzleminden geçtiği noktadır. Yaygın olarak kullanılan referans düzlemleri ve boylamın kökenleri şunları içerir:

  • Yer merkezli yörüngeler için, referans düzlemi olarak Dünya'nın ekvator düzlemi ve boylamın başlangıcı olarak Koç'un ilk noktası. Bu durumda boylam, çıkış düğümün sağ açıklığı (RAAN) olarak da adlandırılır. Açı, Koç'un ilk noktasından düğüme doğuya doğru (veya kuzeyden görüldüğü gibi saat yönünün tersine) ölçülür.[2][3] Bir alternatif, uzay aracının ekvatoru geçtiği yerel ortalama zamana dayanan, çıkış düğümün yerel saatidir (LTAN). Diğer gezegenlerin etrafındaki uydular için de benzer tanımlar mevcuttur (bkz. Gezegen koordinat sistemleri).
  • Güneş merkezli yörüngeler için, referans düzlemi olarak ekliptik ve boylamın başlangıcı olarak Koç'un ilk noktası. Açı, Koç'un ilk noktasından düğüme kadar saat yönünün tersine (ekliptiğin kuzeyinden görüldüğü gibi) ölçülür.[2]
  • Güneş Sistemi dışındaki yörüngeler için, referans düzlemi olarak ilgi noktasında (gök düzlemi olarak adlandırılır) gökküresine teğet olan düzlem ve kuzey (yani, gözlemciden kuzey gök kutbuna yönün dik izdüşümü) gökyüzü düzlemine) boylamın kökeni olarak. Açı, kuzeyden düğüme doğuya doğru (veya gözlemci tarafından görüldüğü gibi saat yönünün tersine) ölçülür.[4], pp. 40, 72, 137; [5], chap. 17.

Sadece görsel gözlemlerden bilinen çift yıldız durumunda, hangi düğümün yükseldiğini ve hangi düğümün alçaldığını söylemek mümkün değildir. Bu durumda kaydedilen yörünge parametresi basitçe düğümün boylamı, Ω olarak etiketlenir ve boylamı 0 ile 180 derece arasında olan düğümün boylamını temsil eder.[5], chap. 17;[4], p. 72.

Durum vektörlerinden hesaplama

Astrodinamikte, yükselen düğümün boylamı, belirli bağıl açısal momentum vektöründen h aşağıdaki gibi hesaplanabilir:

Burada n = ⟨nx, ny, nz⟩ artan düğüme doğru işaret eden bir vektördür. Referans düzleminin xy düzlemi olduğu varsayılır ve boylamın orijini pozitif x ekseni olarak alınır. k, xy referans düzleminin normal vektörü olan birim vektördür (0, 0, 1).

Eğik olmayan yörüngeler için (eğiklik sıfıra eşit), Ω tanımsızdır. Hesaplama için, o zaman, geleneksel olarak, sıfıra eşittir; yani, yükselen düğüm, n'nin pozitif x eksenini göstermesine izin vermeye eşdeğer olan referans yönünde yerleştirilir.

Ayrıca bakınız

Kaynakça

  1. ^ Parameters Describing Elliptical Orbits 9 Ekim 2016 tarihinde Wayback Machine sitesinde arşivlendi., web page, accessed 17 Mayıs 2007.
  2. ^ a b Orbital Elements and Astronomical Terms 3 Nisan 2007 tarihinde Wayback Machine sitesinde arşivlendi., Robert A. Egler, Dept. of Physics, North Carolina State University. Web page, accessed 17 Mayıs 2007.
  3. ^ Keplerian Elements Tutorial 14 Ekim 2002 tarihinde Wayback Machine sitesinde arşivlendi., amsat.org, accessed 17 Mayıs 2007.
  4. ^ a b The Binary Stars, R. G. Aitken, New York: Semi-Centennial Publications of the University of California, 1918.
  5. ^ a b Celestial Mechanics 6 Temmuz 2007 tarihinde Wayback Machine sitesinde arşivlendi., Jeremy B. Tatum, on line, accessed May 17, 2007.

İlgili Araştırma Makaleleri

<span class="mw-page-title-main">Türev</span> Fonksiyonun grafiğine çizilen teğetin eğimini hesaplama tekniğidir.

Matematikte türev, bir fonksiyonun tanımlı olduğu herhangi bir noktada değişim yönünü veya hızını veren temel bir kavramdır. Tek değişkenli bir fonksiyonun tanım kümesinin belli bir noktasında türevi, fonksiyonun grafiğine bu noktada karşılık gelen değerde çizilen teğet doğrunun eğimidir. Teğet doğru, tanım kümesinin bu noktasında fonksiyonun en iyi doğrusal yaklaşımıdır. Bu nedenle türev genellikle anlık değişim oranı ya da daha açık bir ifadeyle, bağımlı değişkendeki anlık değişimin bağımsız değişkendeki anlık değişime oranı olarak tanımlanır. Bir fonksiyonun türevini teorik olarak bulmaya türev alma denilir. Eğer bir fonksiyonun tanım kümesindeki her değerinde hesaplanan türev değerlerini veren başka bir fonksiyon varsa, bu fonksiyona eldeki fonksiyonun türevi denir.

<span class="mw-page-title-main">Tutulum</span>

Tutulum, ekliptik veya tutulum düzlemi ya da ekliptik düzlem, Dünya'nın Güneş etrafındaki yörünge düzlemidir. Dünya'da bulunan bir gözlemcinin bakış açısından, Güneş'in bir yıl boyunca gök küre etrafındaki hareketi, yıldızların arka planına karşı ekliptik boyunca bir yol izler. Ekliptik önemli bir referans düzlemidir ve ekliptik koordinat sisteminin temelidir.

<span class="mw-page-title-main">Enberi açısı</span> uzaydaki bir nesnenin yörüngesini belirtmek için kullanılan yörünge elemanlarından biri

Enberi açısı, ω olarak sembolize edilir ve yörüngede dönen bir cismin Yörünge öğelerinden biridir. Parametrik olarak ω, cismin çıkış düğümünden enberi noktasına kadar olan ve hareket yönünde ölçülen açıdır.

<span class="mw-page-title-main">Vektör</span> büyüklüğü (veya uzunluğu) ve yönü olan geometrik nesne

Matematik, fizik ve mühendislikte, Öklid vektörü veya kısaca vektör sayısal büyüklüğü ve yönü olan geometrik bir objedir. Vektör, genellikle bir doğru parçası ile özdeşleştirilir. Bir başlangıç noktası A ile bir uç noktası B'yi birleştiren bir ok şeklinde görselleştirilir ve ile belirtilir.

<span class="mw-page-title-main">Açısal momentum</span> Fiziksel nicelik

Açısal momentum, herhangi bir cismin dönüş hareketine devam etme isteğinin bir göstergesidir ve bu nicelik cismin kütlesine, şekline ve hızına bağlıdır. Açısal momentum bir vektör birimidir ve cismin belirli eksenler üzerinde sahip olduğu dönüş eylemsizliği ile dönüş hızını ifade eder.

<span class="mw-page-title-main">Yarıçap</span> merkezinden çevresine bir daire veya küre içinde bölüm veya yüzeyi ile uzunluğu

Yarıçap, bir daire veya kürenin özeğinin (merkezinin) çemberine olan mesafesidir. Çapın yarısına eşittir.

<span class="mw-page-title-main">Tork</span> bir kuvvetin nesnenin ekseninde, dayanak noktasında ya da çevresinde dönme eğilimi

Tork, kuvvet momenti ya da dönme momenti, bir cismin bir eksen etrafındaki dönme, bükülme veya burulma eğilimini dönme ekseni merkezine indirgeyerek ölçen fiziksel büyüklüktür. Torkun büyüklüğü moment kolu uzunluğuna, uygulanan kuvvete ve moment kolu ile kuvvet vektörü arasındaki açıya bağlıdır.

<span class="mw-page-title-main">Logaritmik spiral</span>

Logaritmik spiral, doğada sık rastlanan bir spiral çeşididir. İlk olarak 17. yüzyılda René Descartes ve Jakob Bernoulli tarafından tanımlanmış ve incelenmiştir. Bernoulli bu eğriye, kendine özgü matematiksel özelliklerinden dolayı, spira mirabilis adını vermiş ve mezar taşına bir logaritmik spiral oyulmasını vasiyet etmiştir.

Vektör uzayı veya Yöney uzayı, matematikte ölçeklenebilir ve eklenebilir bir nesnelerin (vektörlerin) uzayına verilen isimdir. Daha resmî bir tanımla, bir vektör uzayı, iki elemanı arasında vektör toplamasının ve skaler denilen sayılarla çarpımın tanımlı olduğu ve bunların bazı aksiyomları sağladığı kümedir. Skalerler, rasyonal veya reel sayılar kümesinden gelebilir, ama herhangi bir cisim üzerinden bir vektör uzayı oluşturmak mümkündür. Vektör uzayları, skalerlerin geldiği cisime göre reel vektör uzayı, kompleks vektör uzayı veya genel bir cisim üzerinden K vektör uzayı şeklinde adlandırılır.

<span class="mw-page-title-main">Karmaşık düzlem</span>

Matematikte karmaşık düzlem, gerçel eksen ve ona dik olan sanal eksen tarafından oluşturulmuş, karmaşık sayıların geometrik bir gösterimidir. Karmaşık sayının gerçel kısmının x-ekseni boyuncaki yer değiştirmeyle, sanal kısmının ise y-eksenindeki yer değiştirmeyle temsil edildiği değiştirilmiş bir Kartezyen düzlem olarak düşünülebilir.

Açısal hız, bir objenin birim zamandaki açısal olarak yer değiştirme miktarına verilen isimdir. Açısal hız vektörel olup bir cismin bir eksen üzerindeki dönüş yönünü ve hızını verir. Açısal hızın SI birimi radyan/saniyedir, ancak başka birimlerde de ölçülebilir. Açısal hız genellikle omega sembolü ile gösterilir. Açısal hızın yönü genellikle dönüş düzlemine diktir ve sağ el kuralı ile bulunabilir.

<span class="mw-page-title-main">Öklid uzayı</span> Öklid geometrisinin yüksek boyutlu vektör uzaylarına genelleştirilmesi

Matematikte Öklid uzayı, Öklid geometrisinin üç boyutlu uzayıdır ve bu kavramlar, çok boyutlu olarak genelleştirilir. “Öklid” terimi bu uzayları, Öklid geometrisi olmayan eğimli uzaydan ve Einstein'nın genel görelilik kuramından ayırt eder. Bu adı Yunan matematikçi Öklid'den dolayı almıştır.

<span class="mw-page-title-main">Silindirik ve küresel koordinatlarda vektör alanı</span>

NOT: Bu sayfa küresel koordinatların fizik gösterimi içindir, z ekseni arasındaki açıdır.ve yarıçap vektörü söz konusu noktaya orijinden bağlantılıdır, bu açısı x-y düzlemi ve x ekseni ile vektör yarıçapının izdüşümü arası açıdır. Diğer bazı tanımları da kullanılıyor ve çok dikkatli farklı kaynaklardan karşılaştırarak alınmalıdır.

Matematikte, Green kuramı basit, kapalı bir C eğrisi etrafındaki çizgi integrali ile C eğrisinin sınırlandırdığı D düzlem bölgesi üzerindeki çift katlı integral arasındaki ilişkiyi verir. Teorem adını matematikçi George Green'den almıştır ve daha genel hâli olan Stokes teoreminin iki boyuttaki özel durumudur.

<span class="mw-page-title-main">Kepler yörüngesi</span> üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklayan kavram

Gök mekaniği olarak, Kepler yörüngesi üç boyutlu uzayda iki boyutlu bir yörünge düzlemi oluşturan bir elips, parabol, hiperbol benzeri bir yörünge cismininin hareketini açıklar.. Kepler yörüngesi yalnızca nokta iki cismin nokta benzeri yerçekimsel çekimlerini dikkate alır, atmosfer sürüklemesi, güneş radyasyonu baskısı, dairesel olmayan cisim merkezi ve bunun gibi bir takım şeylerin diğer cisimlerle girdiği çekim ilişkileri nedeniyle ihmal eder. Böylece Kepler problemi olarak bilinen iki-cisim probleminin, özel durumlara bir çözüm olarak atfedilir. Klasik mekaniğin bir teorisi olarak, aynı zamanda genel görelilik etkilerini dikkate almaz. Kepler yörüngeleri çeşitli şekillerde altı yörünge unsurları içine parametrize edilebilir.

Referans düzlemi, gök mekaniğinde yörünge öğelerini tanımlarken kullanılan bir düzlemdir. Referans düzlemine göre tanımlanan iki ana yörünge öğesi yörünge eğikliği ve çıkış düğümü boylamıdır.

<span class="mw-page-title-main">Yörünge düzlemi</span>

Yörünge düzlemi, dönen bir cismin yörüngesinin içinde bulunduğu geometrik bir düzlemdir. Bir yörünge düzlemini belirlemek için üç doğrusal nokta yeterlidir. Büyük bir cismin yörüngesinde hareket etmekte olan bir gökcisminin iki farklı zaman veya noktası bu ölçüme bir referans olabilir.

<span class="mw-page-title-main">Enberi boylamı</span>

Gök mekaniğinde, yörüngedeki bir cismin enberi boylamı, aynı zamanda pericenter boylamı olarak da adlandırılır, cismin yörünge eğiminin sıfır olması durumunda enberinin gerçekleşeceği boylamdır. Genellikle ϖ işaretiyle gösterilir.

<span class="mw-page-title-main">Gerçek anomali</span>

Gerçek anomali, gök mekaniğinde Kepler yörüngesinde hareket etmekte olan bir cismin pozisyonunu belirleyen açısal bir parametredir. Gerçek anomali, bir yörüngedeki çeşitli noktaların konumlarını tanımlamak için kullanılan bir terimdir. Enberi noktası yönü ile elipsin ada odağından görünen cismin mevcut konumu yani nesnenin etrafında döndüğü nokta arasındaki açıyı göstermektedir.

<span class="mw-page-title-main">Yörünge durum vektörleri</span>

Yörünge durum vektörleri veya durum vektörleri, gök mekaniği ve yörünge mekaniğinde, konum ve hız kartezyen vektörlerin zaman (devir) ile birlikte uzaydaki yörüngede bulunan bir cismin benzersiz şekildeki gidim izinin belirlenmesidir.


Bu sayfa, bu Vikipedi makalesine dayanmaktadır.
Metin, CC BY-SA 4.0 lisansı altında mevcuttur; ek koşullar uygulanabilir.
Görseller, videolar ve sesler kendi lisansları altında mevcuttur.